题目内容
【题目】如图1,在路边安装路灯,路宽为OD,灯柱OB长为h米,灯杆AB长为1米,且灯杆与灯柱成120°角,路灯采用圆锥形灯罩,其轴截面的顶角为2θ,灯罩轴线AC与灯杆AB垂直. 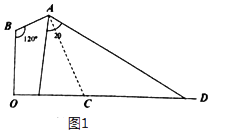
(1)设灯罩轴线与路面的交点为C,若OC=5 ![]() 米,求灯柱OB长;
米,求灯柱OB长;
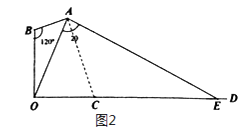
(2)设h=10米,若灯罩轴截面的两条母线所在直线一条恰好经过点O,另一条与地面的交点为E(如图2); 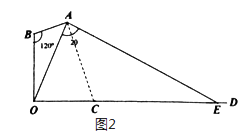
(i)求cosθ的值;
(ii)求该路灯照在路面上的宽度OE的长;
【答案】
(1)解:过A作AE⊥OD,垂足为E,过B作BF⊥AE,垂足为F,
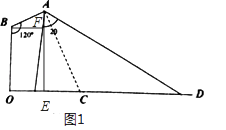
则∠ABF=120°﹣90°=30°,
∴AF= ![]() AB=
AB= ![]() ,BF=
,BF= ![]() AB=
AB= ![]() ,
,
∴OE=BF= ![]() ,
,
∴CE=OC﹣OE= ![]() .
.
在四边形ABOC中,∵∠BOC=∠BAC=90°,∠ABO=120°,
∴∠ACO=60°,
在Rt△ACE中,tan∠ACE= ![]() =
= ![]() ,
,
∴AE= ![]() CE=
CE= ![]() ,
,
∴OB=EF=AE﹣AF=13.
即灯柱OB高13米.
(2)解:(i)在△ABO中,由余弦定理得OA= ![]() =
= ![]() ,
,
由正弦定理得 ![]() =
= ![]() ,∴sin∠BAO=
,∴sin∠BAO= 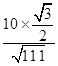 =
= ![]() .
.
∴cosθ=sin∠BAO= ![]() .
.
(ii)sinθ= ![]() =
= ![]() ,sin2θ=2sinθcosθ=
,sin2θ=2sinθcosθ= ![]() ,
,
∴sin∠AEO=sin(60°﹣θ)= ![]() ﹣
﹣ ![]() =
= ![]() .
.
在△AOE中,由正弦定理得 ![]() =
= ![]() ,
,
解得OE= ![]() =
= ![]() .
.
【解析】(1)作AE⊥OD,BF⊥AE,求出AF,BF,得出CE的长,根据tan∠ACE= ![]() 求出AE,从而得出OB的长;(2)(i)在△AOB中,利用正弦定理求出sin∠BAO即可得出cosθ;(ii)利用差角公式计算sin∠AEO,在△AOE中,利用正弦定理计算OE.
求出AE,从而得出OB的长;(2)(i)在△AOB中,利用正弦定理求出sin∠BAO即可得出cosθ;(ii)利用差角公式计算sin∠AEO,在△AOE中,利用正弦定理计算OE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目