题目内容
4. 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是棱DD1、C1D1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是棱DD1、C1D1的中点.(1)求直线BE和平面ABB1A1所成角θ的正弦值;
(2)证明:B1F∥平面A1BE.
分析 (1)取AA1的中点G,并连接GE,BG,从而可说明∠EBG为直线BE和平面ABB1A1所成角,从而θ=∠EBG,可设正方体的边长为a,在直角三角形EBG中,即可求出sinθ=$\frac{GE}{BE}$;
(2)连接FE,C1D,AB1,并设AB1交AB1于H,连接EH,容易说明四边形B1FEH为平行四边形,从而得到B1F∥HE,根据线面平行的判定定理即可得出直线B1F∥平面A1BE.
解答 解:(1)如图,设G是AA1的中点,连接GE,BG;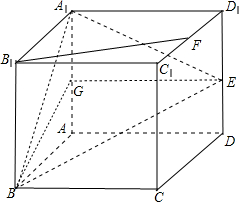 ∵E为DD1的中点,ABCD-A1B1C1D1为正方体;
∵E为DD1的中点,ABCD-A1B1C1D1为正方体;
∴GE∥AD,又∵AD⊥平面ABB1A1;
∴GE⊥平面ABB1A1;
∴Rt△BEG中的∠EBG是直线BE和平面ABB1A1所成角,即∠EBG=θ;
设正方体的棱长为a,∴GE=a,$BG=\frac{{\sqrt{5}}}{2}a$,$BE=\sqrt{B{G^2}+G{E^2}}=\frac{3}{2}a$;
∴直线BE和平面ABB1A1所成角θ的正弦值为:sinθ=$\frac{GE}{BE}=\frac{2}{3}$;
(2)证明:如图,连接EF、AB1、C1D,记AB1与A1B的交点为H,连接EH;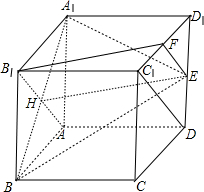
∵H为AB1的中点,且B1H=$\frac{1}{2}$C1D,B1H∥C1D;
而EF=$\frac{1}{2}$C1D,EF∥C1D;
∴B1H∥EF且B1H=EF;
∴四边形B1FEH为平行四边形;
∴B1F∥HE;
又∵B1F?平面A1BE,HE?平面A1BE;
∴B1F∥平面A1BE.
点评 考查平行线中一条垂直于一个平面,另一条也垂直于这个平面,线面角的定义及求法,正弦函数的定义,平行四边形的定义,以及线面平行的判定定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知函数f(x)=$\frac{1}{1-x}$,g(x)=lnx,x0是函数h(x)=f(x)+g(x)的一个零点,若x1∈(1,x0),x2∈(x0,+∞),则( )
| A. | h(x1)<0,h(x2)<0 | B. | h(x1)>0,h(x2)>0 | C. | h(x1)>0,h(x2)<0 | D. | h(x1)<0,h(x2)>0 |
4.ax+y-3=0与曲线y=$\frac{lnx}{x}$在x=1处的切线平行,则a的值为( )
| A. | a=1 | B. | a=-1 | C. | a=2 | D. | a=1 |
16.函数y=4sin(ωx+$\frac{π}{4}$)cos(ωx-$\frac{π}{4}$)-2sin(ωx-$\frac{π}{4}$)•cos(ωx+$\frac{π}{4}$)(ω>0)的图象与直线y=3在y轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,P4…,且|P3P5|=$\frac{π}{2}$,则此函数的递增区间为( )
| A. | [2kπ-$\frac{π}{2}$,2kπ+$\frac{π}{2}$](k∈Z) | B. | [$\frac{kπ}{2}$-$\frac{π}{8}$,$\frac{kπ}{2}$+$\frac{π}{8}$](k∈Z) | ||
| C. | [kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$](k∈Z) | D. | [$\frac{kπ}{2}$,$\frac{kπ}{2}$+$\frac{π}{4}$](k∈Z) |
 如图,在平面直角坐标系xoy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.
如图,在平面直角坐标系xoy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.