题目内容

4．ax+y-3=0与曲线y=$\frac{lnx}{x}$在x=1处的切线平行，则a的值为（　　）
A．a=1B．a=-1C．a=2D．a=1

分析 求出函数的导数，利用导数的几何意义结合直线平行的等价条件，即可得到结论．

解答 解：∵函数在点（1，f（1））处的切线与直线ax+y-3=0平行，
∴切线斜率k=-a，即k=f′（1）=-a，
∵y=f（x）=$\frac{lnx}{x}$，
∴f′（x）=$\frac{1-lnx}{{x}^{2}}$，
即k=f′（1）=1=-a，
解得a=-1，
故选：B．

点评 本题主要考查导数的几何意义的应用以及直线平行的关系，根据导数求出函数的切线斜率是解决本题的关键．

练习册系列答案
相关题目
14．已知椭圆C的中心在坐标原点，焦点在x轴上，椭圆右顶点到直线x+y+$\sqrt{3}$=0的距离为$\sqrt{6}$，离心率e=$\frac{\sqrt{6}}{3}$
（Ⅰ）求椭圆C的方程；
（Ⅱ）已知A为椭圆与y轴负半轴的交点，设直线l：y=x+m，是否存在实数m，使直线l与椭圆有两个不同的交点M、N，是|AM|=|AN|，若存在，求出m的值；若不存在，请说明理由．
15．已知点P为y轴上的动点，点M为x轴上的动点．点F（1，0）为定点，且满足$\overrightarrow{PN}$+$\frac{1}{2}$$\overrightarrow{NM}$=$\overrightarrow{0}$，$\overrightarrow{PM}$•$\overrightarrow{PF}$=0．
（Ⅰ）求动点N的轨迹E的方程．
（Ⅱ）A，B是E上的两个动点，l为AB的中垂线，求当l的斜率为2时，l在y轴上的截距m的范围．
12．专家通过研究学生的学习行为，发现学生的注意力随着老师讲课时间的变化而变化，讲课开始时，学生的兴趣激增，中间有一段时间，学生的兴趣保持较理想的状态，随后学生的注意力开始分散，设f（x）表示学生注意力随时间x（分钟）的变化规律．（f（x）越大，表明学生注意力越大），经过试验分析得知：$f（x）=\left\{\begin{array}{l}-{x^2}+24x+100，0＜x≤10\\ 240，10＜x＜20\\-7x+380，20≤x≤40\end{array}\right.$
（Ⅰ）讲课开始后多少分钟，学生的注意力最集中？能坚持多少分钟？
（Ⅱ）讲课开始后5分钟时与讲课开始后25分钟时比较，何时学生的注意力更集中？
（Ⅲ）一道数学难题，需要讲解24分钟，并且要求学生的注意力至少达到180，那么经过适当安排，老师能否在学生达到所需的状态下讲完这道题目？
19．在等差数列{an}中，a1=3，a17=35，则公差d=（　　）
A．0B．-2C．2D．4
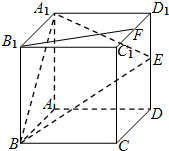9．已知集合A={y|y=x2-2x-3，x∈R}，B={y|y=-x2+2x+13，x∈R}，则∁R（A∩B）=（-∞，-4）∪（14，+∞）．
4．如图所示，在正方体ABCD-A1B1C1D1中，E、F分别是棱DD1、C1D1的中点．
（1）求直线BE和平面ABB1A1所成角θ的正弦值；
（2）证明：B1F∥平面A1BE．
1．在△ABC中，角A，B，C的对边分别为a，b，c，点M（b，a），O为坐标原点，若直线OM与直线l：xsinB+y（sinB-sinA）+（a-c）sinC-asinB=0垂直，垂足为M，则$\frac{c}{a}$=$\frac{1+\sqrt{13}}{2}$．
2．设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F1、F2，短轴长为2，离心率为$\frac{\sqrt{3}}{2}$．
（1）求椭圆的方程；
（2）如图，设直线l1；y=x+m1与椭圆交于A、B两点，直线l2：y=x+m2与椭圆交于C、D两点，若四边形ABCD是平行四边形，求四边形ABCD的面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网