题目内容
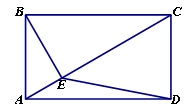
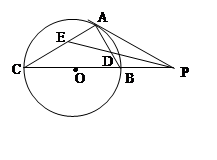
(本小题满分10分)选修4-1:几何证明讲 如图,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA的延长线于点F.

求证:(1)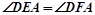 ;
;
(2)AB2=BE•BD-AE•AC.

求证:(1)
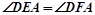 ;
;(2)AB2=BE•BD-AE•AC.
(1)连结AD所以∠ADB=90°又EF⊥AB,∠EFA=90°则A、D、E、F四点共圆,∴∠DEA=∠DFA(2)由(1)知,BD•BE=BA•BF,又△ABC∽△AEF∴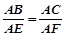 即:AB•AF=AE•AC
即:AB•AF=AE•AC
∴ BE•BD-AE•AC=BA•BF-AB•AF=AB(BF-AF)=AB2
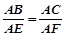 即:AB•AF=AE•AC
即:AB•AF=AE•AC∴ BE•BD-AE•AC=BA•BF-AB•AF=AB(BF-AF)=AB2
试题分析:(1) 连结AD
因为AB为圆的直径,所以∠ADB=90°,又EF⊥AB,∠EFA=90°
则A、D、E、F四点共圆
∴∠DEA=∠DFA
(2) 由(1)知,BD•BE=BA•BF
又△ABC∽△AEF
∴
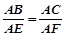
即:AB•AF=AE•AC
∴ BE•BD-AE•AC
=BA•BF-AB•AF
=AB(BF-AF)
=AB2
点评:与圆相关的证明角相等问题结合圆中的性质,圆中相等的角构成的相似三角形边的长度比例关系

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
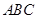 的顶点坐标
的顶点坐标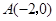 ,直角顶点
,直角顶点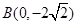 ,顶点
,顶点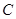 在
在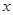 轴上,点
轴上,点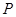 为线段
为线段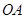 的中点
的中点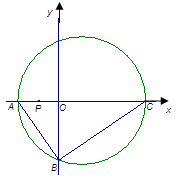
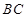 边所在直线方程;
边所在直线方程; 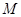 为直角三角形
为直角三角形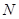 过点
过点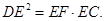

 0的切线,A为切点,PBC是过点O的割线,PA ="10,PB" =5、
0的切线,A为切点,PBC是过点O的割线,PA ="10,PB" =5、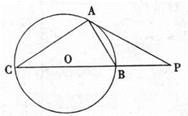
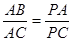 ;
;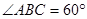 ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长.
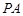 与圆
与圆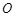 相切于点
相切于点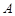 ,经过点
,经过点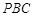 交圆
交圆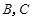 ,
,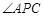 的平分线分别交
的平分线分别交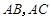 于点
于点 .
.
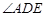 =
=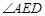 ;
;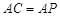 ,求
,求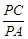 的值.
的值.
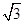 ,PC=1,则圆O的半径为________ .
,PC=1,则圆O的半径为________ .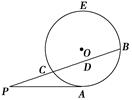
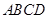 中,
中,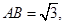
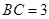 ,
,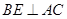 ,垂足为
,垂足为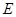 ,则
,则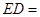 .
.