题目内容
19．三棱锥P-ABC的四个顶点都在半径为5的球面上，底面ABC所在的小圆面积为16π，则该三棱锥的高的最大值为（ ）| A． | 7 | B． | 7.5 | C． | 8 | D． | 9 |
分析 由小圆面积为16π，可以得小圆的半径；由图知三棱锥高的最大值应过球心，故可以作出解答．
解答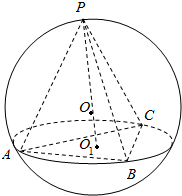 
解：设小圆半径为r，则πr2=16π，∴r=4．
显然，当三棱锥的高过球心O时，取得最大值；
由OO1=$\sqrt{{5}^{2}-{4}^{2}}$=3，∴高PO1=PO+OO1=5+3=8．
故选C．
点评 本题考查了由圆的面积求半径，以及勾股定理的应用，是基础题．
练习册系列答案
相关题目
9．已知命题p：函数f（x）=sinxcosx的单调递增区间[$kπ-\frac{π}{4}$，$kπ+\frac{π}{4}$]（k∈Z）；命题q：函数g（x）=sin（x+$\frac{π}{2}$） 的图象关于原点对称，则下列命题中为真命题的是（ ）
| A． | p∧q | B． | p∨q | C． | -p | D． | （-p）∨q |
10．若圆C1的方程是x2+y2-4x-4y+7=0，圆C2的方程为x2+y2-4x-10y+13=0，则两圆的公切线有（ ）
| A． | 2条 | B． | 3条 | C． | 4条 | D． | 1条 |
7．若a∈R，则“a2＞a”是“a＞1”的（ ）条件．
| A． | 充分不必要 | B． | 必要不充分 | ||
| C． | 充要 | D． | 既不充分也不必要 |
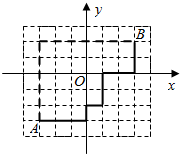现代城市大多是棋盘式布局（如上海道路几乎都是东西和南北走向）．在这样的城市中，我们说的两点间的距离往往不是指两点间的直线距离（位移），而是实际路程（如图）．在直角坐标平面内，我们定义A（x1，y1）、B（x2，y2）两点间的“直角距离”为：D（AB）=|x1-x2|+|y1-y2|．