题目内容
5．由命题p：“函数y=$\frac{1}{x}$是减函数”与q：“数列a、a2、a3…是等比数列”构成的复合命题，下列判断正确的是（ ）| A． | p或q为真，p且q为假，非p为真 | B． | p或q为假，p且q为假，非p为真 | ||
| C． | p或q为真，p且q为假，非p为假 | D． | p或q为假，p且q为真，非p为真 |
分析 根据反比例函数的图象和性质，可判断命题p的真假；根据等比数列的定义，可判断命题q的真假，进而根据复合命题真假判断的真值表，可得答案．
解答 解：命题p：“函数y=$\frac{1}{x}$是减函数”为假命题，
命题q：“数列a、a2、a3…是等比数列”为假命题，（a可能为0），
故p或q为假，p且q为假，非p为真，
故选：B
点评 本题考查的知识点是复合命题的真假判断，其中判断简单命题的真假是解答的关键．
练习册系列答案
相关题目
15．已知实数a，b，c满足不等式0＜a＜b＜c＜1，且M=2a，N=5-b，P=lnc，则M、N、P的大小关系为（ ）
| A． | P＜N＜M | B． | P＜M＜N | C． | M＜P＜N | D． | N＜P＜M |
10．
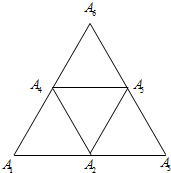如图，由四个边长为1的等边三角形拼成一个边长为2的等边三角形，各项点依次为，A1，A2，A3，…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}}，（{i，j∈[{1，2，3，…6}]}）$的值组成的集合为（ ）
如图，由四个边长为1的等边三角形拼成一个边长为2的等边三角形，各项点依次为，A1，A2，A3，…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}}，（{i，j∈[{1，2，3，…6}]}）$的值组成的集合为（ ）| A． | {-2，-1，0，1，2} | B． | $\left\{{-2，-1，-\frac{1}{2}，0，\frac{1}{2}，1，2}\right\}$ | ||
| C． | $\left\{{-\frac{3}{2}，-1，-\frac{1}{2}，0，\frac{1}{2}，1，\frac{3}{2}}\right\}$ | D． | $\left\{{-2，-\frac{3}{2}，-1，-\frac{1}{2}，0，\frac{1}{2}，1，\frac{3}{2}，2}\right\}$ |
1．公差不为零的等差数列{an}的前n项和为Sn，若a3是a2与a6的等比中项，则$\frac{S_3}{a_3}$=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | 1 | D． | 2 |