题目内容
【题目】同时具有性质:“① 最小正周期是![]() ;② 图象关于直线
;② 图象关于直线![]() 对称;③ 在
对称;③ 在![]() 上是单调递增函数”的一个函数可以是( )
上是单调递增函数”的一个函数可以是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
利用正弦函数、余弦函数的图象和性质,逐一检验,可得结论.
A,对于y=cos(![]() ),它的周期为
),它的周期为![]() 4π,故不满足条件.
4π,故不满足条件.
B,对于y=sin(2x![]() ),在区间
),在区间![]() 上,2x
上,2x![]() ∈[
∈[![]() ,
,![]() ],故该函数在区间
],故该函数在区间![]() 上不是单调递增函数,故不满足条件.
上不是单调递增函数,故不满足条件.
C,对于y=cos(2x![]() ),当x
),当x![]() 时,函数y
时,函数y![]() ,不是最值,故不满足②它的图象关于直线x
,不是最值,故不满足②它的图象关于直线x![]() 对称,故不满足条件.
对称,故不满足条件.
D,对于y=sin(2x![]() ),它的周期为
),它的周期为![]() π,当x
π,当x![]() 时,函数y=1,是函数的最大值,满足它的图象关于直线x
时,函数y=1,是函数的最大值,满足它的图象关于直线x![]() 对称;且在区间
对称;且在区间![]() 上,2x
上,2x![]() ∈[
∈[![]() ,
,![]() ],故该函数在区间
],故该函数在区间![]() 上是单调递增函数,满足条件.
上是单调递增函数,满足条件.
故选:D.

练习册系列答案
相关题目
【题目】某单位响应党中央“精准扶贫”号召,对某村6户贫困户中的甲户进行定点帮扶,每年跟踪调查统计一次,从2015年1月1日至2018年12月底统计数据如下(人均年纯收入):
年份 | 2015年 | 2016年 | 2017年 | 2018年 |
年份代码 | 1 | 2 | 3 | 4 |
收入 | 25 | 28 | 32 | 35 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计甲户在2019年能否脱贫;(国家规定2019年脱贫标准:人均年纯收入为3747元)
,并估计甲户在2019年能否脱贫;(国家规定2019年脱贫标准:人均年纯收入为3747元)
(2)2019年初,根据扶贫办的统计知,该村剩余5户贫困户中还有2户没有脱贫,现从这5户中抽取2户,求至少有一户没有脱贫的概率.
参考公式: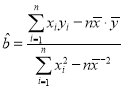 ,
,![]() ,其中
,其中![]() ,
,![]() 为数
为数![]() ,
,![]() 的平均数.
的平均数.