题目内容
于直线m、n与平面α、β,有下列四个命题:
①若m∥α,n∥β且α∥β,则m∥n;
②若m⊥α,n⊥β且α⊥β,则m⊥n;
③若m⊥α,n∥β且α∥β,则m⊥n;
④若m∥α, n⊥β且α⊥β,则m∥n.
其中真命题的序号是( )
①若m∥α,n∥β且α∥β,则m∥n;
②若m⊥α,n⊥β且α⊥β,则m⊥n;
③若m⊥α,n∥β且α∥β,则m⊥n;
④若m∥α, n⊥β且α⊥β,则m∥n.
其中真命题的序号是( )
| A.①② | B.③④ | C.①④ | D.②③ |
D
本题考查线线、线面、面面平行,垂直的判定和性质.①④错误可以通过反例证明.
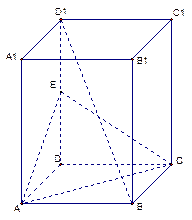
如图(1),①利用正方体模型α∥β,?m∥α,n∥β,但M与n不平行.∴①错误.
如图(2),④m∥α,n⊥β,α⊥β,但M与n相交.
如图(3),②设α∩β=l,在l上任取一点O,在平面α内,过点O作n′⊥l;
在平面β内,过点O作M′⊥l.
∵α⊥β,∴n′⊥β,m′⊥α.
∵m⊥α,n⊥β,
∴m′∥M,n′∥n.
∴m与n所成的角为m′与n′所成的角.
∵m′⊥α,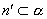 ,
,
∴m′⊥n′.∴m⊥n.

如图(4),③∵n∥β,
∴过n作平面γ使γ∩β=n′,
∴n∥n′.
∵α∥β,m⊥α,∴M⊥β.
∵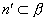 ,∴m⊥n′.∴m⊥n.
,∴m⊥n′.∴m⊥n.
∴②③正确.
如图(1),①利用正方体模型α∥β,?m∥α,n∥β,但M与n不平行.∴①错误.

如图(2),④m∥α,n⊥β,α⊥β,但M与n相交.
如图(3),②设α∩β=l,在l上任取一点O,在平面α内,过点O作n′⊥l;
在平面β内,过点O作M′⊥l.
∵α⊥β,∴n′⊥β,m′⊥α.
∵m⊥α,n⊥β,
∴m′∥M,n′∥n.
∴m与n所成的角为m′与n′所成的角.
∵m′⊥α,
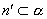 ,
,∴m′⊥n′.∴m⊥n.

如图(4),③∵n∥β,
∴过n作平面γ使γ∩β=n′,
∴n∥n′.
∵α∥β,m⊥α,∴M⊥β.
∵
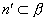 ,∴m⊥n′.∴m⊥n.
,∴m⊥n′.∴m⊥n.∴②③正确.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 平面
平面 ,
, 、
、 是夹在两条平行平面间的两条线段,
是夹在两条平行平面间的两条线段,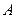 、
、 在
在 内,
内, 、
、 在
在 、
、 分别在
分别在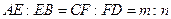 .求证:
.求证: .
.
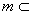 平面β,给出下列命题:
平面β,给出下列命题:  l∥M;
l∥M; ∶S△ABC.
∶S△ABC. 平面ABCD且直线FG∥直线A1B1.
平面ABCD且直线FG∥直线A1B1. 中,
中, ,
, ,且
,且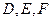 分别为
分别为 的中点.
的中点. ;
; 上是否存在一点
上是否存在一点 ,使得
,使得 ∥平面
∥平面 ?证明
?证明 你的结论.
你的结论.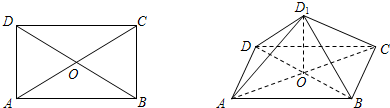
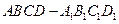
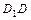
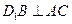 ;
;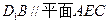 .
.