Question

【题目】圆内有一点P(－1,2)，AB为过点P且倾斜角为的弦．

(1)当时，求AB的长；

(2)当弦AB被点P平分时，写出直线AB的方程．

Answer 1

【答案】（1）（6′）依题意直线AB的斜率为-1，直线AB的方程为：y-2=-(x+1),圆心O(0,0)到直线AB的距离为d=,则AB==,AB的长为.

（2）（6′）当弦AB被点P平分时，弦AB与OP垂直，此时OP的斜率为-2，所以AB的斜率为,根据点斜式方程直线AB的方程为x-2y+5=0.

【解析】

(1)过点O做OG⊥AB于G,连接OA,依题意可知直线AB的斜率,求得AB的

方程,利用点到直线的距离求得OG，由圆的半径进而求得OA的长,则OB可求得;

(2)弦AB被P平分时,OP⊥AB,则OP的斜率可知,利用点斜式求得AB的方程.

(1) 过点O做OG⊥AB于G,连接OA;过点P（-1，2）的直线AB倾斜角

直线AB斜率-1，则直线AB的方程是：y=-x+1

圆的半径

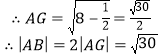
（2））当弦被点P平分时， 此时直线OP的斜率-2，

则直线AB的斜率为 ，

由直线的点斜式方程可知，直线AB的方程为：

即直线AB的方程为：x-2y+5 =0