题目内容
【题目】已知椭圆Г: ![]() (a>b>0)的左、右焦点分别为F1 , F2 , 离心率为
(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为 ![]() ,F2与椭圆上点的连线的中最短线段的长为
,F2与椭圆上点的连线的中最短线段的长为 ![]() ﹣1.
﹣1.
(1)求椭圆Г的标准方程;
(2)已知Г上存在一点P,使得直线PF1 , PF2分别交椭圆Г于A,B,若 ![]() =2
=2 ![]() ,
, ![]() =λ
=λ ![]() (λ>0),求λ的值.
(λ>0),求λ的值.
【答案】
(1)解:由题意可得: ![]() =
= ![]() ,a﹣c=
,a﹣c= ![]() ﹣1,b2=a2﹣c2,解得:a2=2,c=1,b=1.
﹣1,b2=a2﹣c2,解得:a2=2,c=1,b=1.
∴椭圆Г的标准方程为 ![]() +y2=1
+y2=1
(2)解:设A(x1,y1),B(x2,y2),点P(x0,y0),直线PA的方程:x=my﹣1,
联立 ![]() ,化为:(m2+2)y2﹣2my﹣1=0,
,化为:(m2+2)y2﹣2my﹣1=0,
∴y0y1= ![]() ,x0=my0﹣1,
,x0=my0﹣1,
∴m= ![]() .
.
∴ ![]() =﹣
=﹣ ![]() =﹣
=﹣ 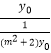 =
= ![]() =
= ![]()
![]() =
= ![]() +2
+2 ![]() =
= ![]() +2
+2 ![]() =3+2x0.
=3+2x0.
∴3+2x0=2,解得x0=﹣ ![]() ,∴P
,∴P ![]() .
.
(i)当取P ![]() 时,
时, ![]() =
= ![]() =﹣
=﹣ ![]() ,可得直线PF2的方程:y=﹣
,可得直线PF2的方程:y=﹣ ![]() (x﹣1),即x=﹣
(x﹣1),即x=﹣ ![]() y+1.
y+1.
代入椭圆方程可得: ![]() y2﹣
y2﹣ ![]() y﹣1=0,∴y2y0=﹣
y﹣1=0,∴y2y0=﹣ ![]() ,而y0=
,而y0= ![]() ,
,
∴y2=﹣ ![]() ,∴
,∴ ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() =4,即λ=4.
=4,即λ=4.
(ii)当P ![]() 时,同理可得:λ=4.
时,同理可得:λ=4.
综上可得:λ=4
【解析】(1)由题意可得: ![]() =
= ![]() ,a﹣c=
,a﹣c= ![]() ﹣1,b2=a2﹣c2 , 联立解出即可得出椭圆Г的标准方程.(2)设A(x1 , y1),B(x2 , y2),点P(x0 , y0),直线PA的方程:x=my﹣1,与椭圆方程联立化为:(m2+2)y2﹣2my﹣1=0,可得y0y1=
﹣1,b2=a2﹣c2 , 联立解出即可得出椭圆Г的标准方程.(2)设A(x1 , y1),B(x2 , y2),点P(x0 , y0),直线PA的方程:x=my﹣1,与椭圆方程联立化为:(m2+2)y2﹣2my﹣1=0,可得y0y1= ![]() ,x0=my0﹣1,解得m=
,x0=my0﹣1,解得m= ![]() .可得
.可得 ![]() =﹣
=﹣ ![]() =3+2x0=2.解得x0 , 可得P坐标.利用点斜式可得直线PF2的方程,代入椭圆方程可即可得出.
=3+2x0=2.解得x0 , 可得P坐标.利用点斜式可得直线PF2的方程,代入椭圆方程可即可得出.
【考点精析】通过灵活运用椭圆的标准方程,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 即可以解答此题.
即可以解答此题.