题目内容
【题目】如图,在三棱锥![]() 中,
中,![]() 分别为棱
分别为棱![]() 的中点.已知
的中点.已知![]() ,
,![]() .
.
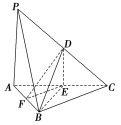
求证:(1)直线PA![]() 平面DEF;
平面DEF;
(2)平面BDE⊥平面ABC.
【答案】(1)见解析(2)见解析
【解析】
试题分析:(1) 由线面平行的判定定理可知,只须证PA与平面DEF内的某一条直线平行即可,由已知及图形可知应选择DE,由三角形的中位线的性质易知: DE∥PA ,从而问题得证;注意线PA在平面DEG外,而DE在平面DEF内必须写清楚;(2) 由面面垂直的判定定理可知,只须证两平中的某一直线与另一个平面垂直即可,注意题中已知了线段的长度,那就要注意利用勾股定理的逆定理来证明直线与直线的垂直;通过观察可知:应选择证DE垂直平面ABC较好,由(1)可知:DE⊥AC,再就只须证DE⊥EF即可;这样就能得到DE⊥平面ABC,又DE![]() 平面BDE,从面而有平面BDE⊥平面ABC.
平面BDE,从面而有平面BDE⊥平面ABC.
试题解析:(1)因为D,E分别为PC,AC的中点,所以DE∥PA.
又因为PA![]() 平面DEF,DE
平面DEF,DE![]() 平面DEF,所以直线PA∥平面DEF.
平面DEF,所以直线PA∥平面DEF.
(2)因为D,E,F分别人棱PC,AC,AB的中点,PA=6,BC=8,所以DE∥PA,DE=![]() PA=3,EF=
PA=3,EF=![]() BC=4.
BC=4.
又因为DF=5,故DF2=DE2+EF2,所以∠DEF=90。,即DE⊥EF.又PA⊥AC,DE∥PA,所以DE⊥AC.
因为AC∩EF=E,AC![]() 平面ABC,EF
平面ABC,EF![]() 平面ABC,所以DE⊥平面ABC.
平面ABC,所以DE⊥平面ABC.
又DE![]() 平面BDE,所以平面BDE⊥平面ABC.
平面BDE,所以平面BDE⊥平面ABC.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目