题目内容
【题目】已知不等式![]() 的解集为
的解集为![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 的解集为
的解集为![]() ,不等式
,不等式![]() 的解集为
的解集为![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)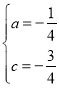 ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)利用一元二次不等式的解集与相应的一元二次方程的实数根的关系即可求出;(2)“![]() ”是“
”是“![]() ”的充分不必要条件,将它们对应的不等式分别解出,可得集合
”的充分不必要条件,将它们对应的不等式分别解出,可得集合![]() 从而建立关于
从而建立关于![]() 的不等关系,解关于
的不等关系,解关于![]() 不等式即可得到实数
不等式即可得到实数![]() 的取值范围.
的取值范围.
试题解析:(1)依题意得,1、3是方程![]() 的两根,且
的两根,且![]() ,...............1分
,...............1分
所以,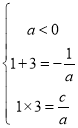 ............................. 3分
............................. 3分
解得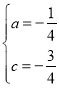 ;................... 5分
;................... 5分
(2)由(1)得![]() ,所以,
,所以,![]() 即为
即为![]() ,
,
解得,![]() ,∴
,∴![]() ,
,
又![]() ,即为
,即为![]() 解得
解得![]() ,∴
,∴![]() ,............8分
,............8分
∵![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() ...............10分
...............10分

练习册系列答案
相关题目