题目内容
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的方程为
的方程为![]() ,动圆
,动圆![]() 过点
过点![]() 和点
和点![]() .记两个圆的交点为
.记两个圆的交点为![]() 、
、![]() .
.
(1)如果直线![]() 的方程为
的方程为![]() ,求圆
,求圆![]() 的方程;
的方程;
(2)当动圆![]() 的面积最小时,求两个圆心距离
的面积最小时,求两个圆心距离![]() 的大小.
的大小.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)联立AB的方程和圆![]() 求得A和B的坐标,求出以点(3,0)和(1,0)为端点的弦的中垂线
求得A和B的坐标,求出以点(3,0)和(1,0)为端点的弦的中垂线![]() ,弦AB的中垂线方程为
,弦AB的中垂线方程为![]() ,联立解得
,联立解得![]() 的圆心坐标为(1,4),由此写出
的圆心坐标为(1,4),由此写出![]() 的方程;
的方程;
(2)当点(3,0)和点(1,0)为圆![]() 直径的两个端点时动圆
直径的两个端点时动圆![]() 的面积最小,求出
的面积最小,求出![]() 的坐标,利用两点间的距离公式求得两个圆心距离
的坐标,利用两点间的距离公式求得两个圆心距离![]() 的大小.
的大小.
解:(1)联立![]() ,
,
解得A和B的坐标分别为(1,0)和(3,2).
∵圆心在以(3,0)和(1,0)为端点的弦的中垂线上,
以点(3,0)和(1,0)为端点的弦的中垂线为![]() ,
,
弦AB的中垂线方程为![]() ,
,
联立解得![]() 的圆心坐标为(1,4),半径为
的圆心坐标为(1,4),半径为![]() ,
,
由此写出![]() 的方程为
的方程为![]() ;
;
(2)动圆![]() 的面积最小,则圆
的面积最小,则圆![]() 的圆心为点(3,0)和点(1,0)连线的中点.
的圆心为点(3,0)和点(1,0)连线的中点.
由中点坐标公式得![]() (1,0),又
(1,0),又![]() (2,1),
(2,1),![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某书店销售刚刚上市的某高二数学单元测试卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如下数据:
单价x/元 | 18 | 19 | 20 | 21 | 22 |
销量y/册 | 61 | 56 | 50 | 48 | 45 |
(1)求试销![]() 天的销量的方差和
天的销量的方差和![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
附: 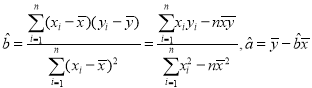 .
.
(2)预计以后的销售中,销量与单价服从上题中的回归直线方程,已知每册单元测试卷的成本是10元,为了获得最大利润,该单元测试卷的单价应定为多少元?