Question

【题目】如图，在△ABC中，已知∠ABC=45°，O在AB上，且OB=OC= AB，又PO⊥平面ABC，DA∥PO，DA=AO= PO．
（Ⅰ）求证：PD⊥平面COD；
（Ⅱ）求二面角B﹣DC﹣O的余弦值．

Answer 1

【答案】证明：（Ⅰ）设OA=1，则PO=OB=2，DA=1， 由DA∥PO，PO⊥平面ABC，知DA⊥平面ABC，
∴DA⊥AO．从而 ，
在△PDO中，∵PO=2，
∴△PDO为直角三角形，故PD⊥DO．
又∵OC=OB=2，∠ABC=45°，
∴CO⊥AB，又PO⊥平面ABC，
∴PO⊥OC，
又PO，AB平面PAB，PO∩AB=O，
∴CO⊥平面PAB．
故CO⊥PD．
∵CO∩DO=O，
∴PD⊥平面COD．
（Ⅱ）解：以OC，OB，OP所在射线分别为x，y，z轴，建立直角坐标系如图．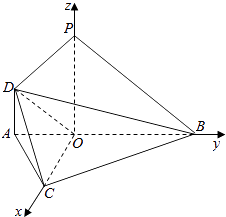

则由（Ⅰ）知，C（2，0，0），B（0，2，0），P（0，0，2），D（0，﹣1，1），
∴ ，
由（Ⅰ）知PD⊥平面COD，∴ 是平面DCO的一个法向量，
设平面BDC的法向量为 ，∴ ，∴ ，
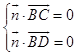令y=1，则x=1，z=3，∴ ，
∴ ，
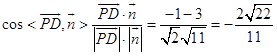由图可知：二面角B﹣DC﹣O为锐角，二面角B﹣DC﹣O的余弦值为 ．
【解析】（Ⅰ）设OA=1，则PO=OB=2，DA=1，由DA∥PO，PO⊥平面ABC，知DA⊥平面ABC，可得DA⊥AO．利用勾股定理的逆定理可得：PD⊥DO．由OC=OB=2，∠ABC=45°，可得CO⊥AB，又PO⊥平面ABC，可得PO⊥OC，得到CO⊥平面PAB．得到CO⊥PD．即可证明．（Ⅱ）如图建立空间直角坐标系，点A为坐标原点，设AB=1，利用线面垂直的性质、向量垂直与数量积的关系得出两个平面的法向量，求出其夹角即可．
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．