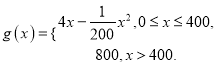题目内容
【题目】设函数![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 存在极值,对于任意的
存在极值,对于任意的![]() ,存在正实数
,存在正实数![]() ,使得
,使得![]() ,试判断
,试判断![]() 与
与![]() 的大小关系并给出证明.
的大小关系并给出证明.
【答案】(Ⅰ)当![]() 时,
时,![]() 在
在![]() 上单调递增.当
上单调递增.当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.(Ⅱ)详见解析
上单调递减.(Ⅱ)详见解析
【解析】【试题分析】(Ⅰ)依据题设条件先求导,再分类讨论探求;(Ⅱ)借助题设条件,运用等价转化与化归的数学思想进行转化,然后再运用导数的知识分析探求:
解(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,![]() .
.
当![]() 时,则
时,则![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
当![]() 时,则由
时,则由![]() 得,
得,![]() ,
,![]() (舍去).当
(舍去).当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .所以
.所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递增.
上单调递增.
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(Ⅱ)由(Ⅰ)知,当![]() 时,
时,![]() 存在极值.
存在极值.

![]() .
.
由题设得![]() .
.
又![]() ,所以
,所以![]()
![]()
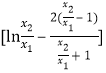 .设
.设![]() ,则
,则![]() ,则
,则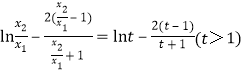 .
.
令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,故
,故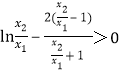 .
.
又因为![]() ,因此
,因此![]() ,即
,即![]() .
.
又由![]() 知
知![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,即
,即![]() .
.

【题目】某种商品在![]() 天每件的销售价格
天每件的销售价格![]() (元)与时间
(元)与时间![]() (天)的函数关系用如图表示,该商品在
(天)的函数关系用如图表示,该商品在![]() 天内日销售量
天内日销售量![]() (件)与时间
(件)与时间![]() (天)之间的关系如下表:
(天)之间的关系如下表:
|
|
|
|
|
|
|
|
|
|

(![]() )根据提供的图象(如图),写出该商品每件的销售价格
)根据提供的图象(如图),写出该商品每件的销售价格![]() 与时间
与时间![]() 的函数关系式.
的函数关系式.
(![]() )根据表
)根据表![]() 提供的数据,写出日销售量
提供的数据,写出日销售量![]() 与时间
与时间![]() 的一次函数关系式.
的一次函数关系式.
(![]() )求该商品的日销售金额的最大值,并指出日销售金额最大的一天是
)求该商品的日销售金额的最大值,并指出日销售金额最大的一天是![]() 天中的第几天.(日销售金额
天中的第几天.(日销售金额![]() 每件的销售价格
每件的销售价格![]() 日销售量)
日销售量)
【题目】随着移动互联网时代的到来,手机的使用非常普遍,“低头族”随处可见。某校为了解家长和教师对学生带手机进校园的态度,随机调查了100位家长和教师,得到情况如下表:
教师 | 家长 | |
反对 | 40 | 20 |
支持 | 20 | 20 |
(1)是否有95%以上的把握认为“带手机进校园与身份有关”,并说明理由;
(2)把以上频率当概率,随机抽取3位教师,记其中反对学生带手机进校园的人数为X,求随机变量X的分布列和数学期望.
附: 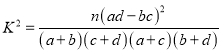
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |