题目内容
【题目】设函数![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )的图象在点
)的图象在点![]() 处的切线的斜率为
处的切线的斜率为![]() ,且函数
,且函数![]() 为偶函数.若函数
为偶函数.若函数![]() 满足下列条件:①
满足下列条件:①![]() ;②对一切实数
;②对一切实数![]() ,不等式
,不等式![]() 恒成立.
恒成立.
(1)求函数![]() 的表达式;
的表达式;
(2)设函数![]() (
(![]() )的两个极值点
)的两个极值点![]() ,
,![]() (
(![]() )恰为
)恰为![]() 的零点,当
的零点,当![]() 时,求
时,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由已知可得![]() ,由
,由![]() 为偶函数
为偶函数![]()
![]() .又
.又![]()
![]()
![]() ,又
,又![]() 恒成立
恒成立![]()
![]() 恒成立
恒成立
![]()
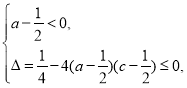
![]()
![]()
![]()
![]() ;(2)由(1)得,
;(2)由(1)得,![]()
![]()
![]()
![]()
![]()
![]() 由题意得
由题意得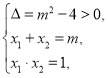
![]()
![]()
![]()
![]() ,
,![]() (
(![]() )
)![]()
![]()
![]()
![]() ,又
,又![]()
![]()
![]()
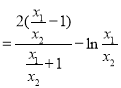 ,设
,设![]() (
(![]() ),
),![]()
![]()
![]() (
(![]() )记为
)记为![]() ,利用导数工具求得
,利用导数工具求得![]()
![]()
![]() 的最小值为
的最小值为![]() .
.
试题解析: (1)由已知可得![]() ,
,
∵函数![]() 为偶函数,
为偶函数,
∴![]() ,
,
即![]() 恒成立,
恒成立,
所以![]() . 又
. 又![]() ,∴
,∴![]() ,
,![]() ,
,
又∵对一切实数![]() ,不等式
,不等式![]() 恒成立,
恒成立,
∴![]() 恒成立,
恒成立,
∴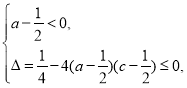
∴![]() ,∴
,∴![]() .
.
(2)由(1)得,![]() ,
,
∴![]() (
(![]() ),
),![]() ,
,
由题意得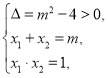 又
又![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∵![]() ,
,![]() (
(![]() )为
)为![]() 的零点,
的零点,
∴![]()
![]() ,
,![]() ,
,
两式相减得,![]()
![]() ,
,
又![]() ,从而
,从而
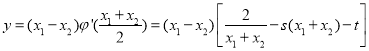
![]()
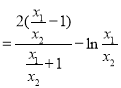 , 设
, 设![]() (
(![]() ),
),
则![]()
![]() (
(![]() )记为
)记为![]() ,
,
![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,
,
故![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目
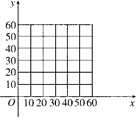
【题目】某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x元与日销售量y件之间有如下所表示的关系.
x | … | 30 | 40 | 45 | 50 | … |
y | … | 60 | 30 | 15 | 0 | … |
(1)在所给的坐标系中,如图,根据表格提供的数据描出实数对(x,y)的对应点,并确定y与x的一个函数关系式y=f(x);
(2)设经营此商品的日销售利润为P元,根据上述关系,写出P关于x的函数关系式,并指出销售单价x为多少时,才能获得最大日销售利润?