题目内容
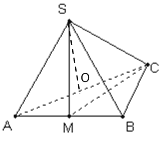
【题目】如图,在三棱锥![]() 中,
中,![]() 是边长为4的正三角形,
是边长为4的正三角形, ![]() ,
,![]() 分别为
分别为![]() 的中点,且
的中点,且![]() .
.
(1)证明:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析(2)![]() (3)
(3)![]()
【解析】
(1)通过证明线线垂直即可得线面垂直.(2) 建立空间直角坐标系,求出两平面法向量的坐标,求其夹角即可.(3)![]() 为平面
为平面![]() 的一个法向量,点B到平面SCM的距离d=
的一个法向量,点B到平面SCM的距离d=![]() 即可得解.
即可得解.
(1)证明:取线段![]() 的中点
的中点![]() ,连接
,连接![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() 且 SO⊥AB,
且 SO⊥AB,
所以![]() 平面
平面![]() .
.
(2)建立如图所示空间直角坐标系,则![]() ,
,
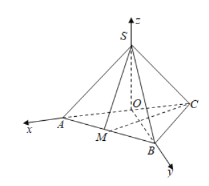
![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
由(1)得:![]() ,
,![]() .
.
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则
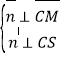 即
即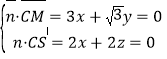
取![]() ,则
,则![]()
![]()
所以![]()
由图可知:二面角![]() 是锐角二面角,
是锐角二面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(3)由(1)(2)可得:![]() ,
,![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
所以,点![]() 到平面
到平面![]() 的距离
的距离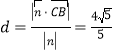

【题目】网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁. 
(1)根据已知条件完成下面的2×2列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?
网购迷 | 非网购迷 | 合计 | |
年龄不超过40岁 | |||
年龄超过40岁 | |||
合计 |
(2)若从网购迷中任意选取2名,求其中年龄丑啊过40岁的市民人数ξ的分布列与期望. 附: ![]() ;
;
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.01 |
k0 | 2.072 | 2.706 | 3.841 | 6.635 |
【题目】某省高考改革新方案,不分文理科,高考成绩实行“3+3”的构成模式,第一个“3”是语文、数学、外语,每门满分150分,第二个“3”由考生在思想政治、历史、地理、物理、化学、生物6个科目中自主选择其中3个科目参加等级性考试,每门满分100分,高考录取成绩卷面总分满分750分.为了调查学生对物理、化学、生物的选考情况,将“某市某一届学生在物理、化学、生物三个科目中至少选考一科的学生”记作学生群体S,从学生群体S中随机抽取了50名学生进行调查,他们选考物理,化学,生物的科目数及人数统计如表:
选考物理、化学、生物的科目数 | 1 | 2 | 3 |
人数 | 5 | 25 | 20 |
(I)从所调查的50名学生中任选2名,求他们选考物理、化学、生物科目数量不相等的概率;
(II)从所调查的50名学生中任选2名,记X表示这2名学生选考物理、化学、生物的科目数量之差的绝对值,求随机变量X的分布列和数学期望;
(III)将频率视为概率,现从学生群体S中随机抽取4名学生,记其中恰好选考物理、化学、生物中的两科目的学生数记作Y,求事件“y≥2”的概率.
