题目内容
已知直线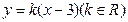 与双曲线
与双曲线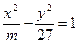 。某学生做了如下变形:由方程组
。某学生做了如下变形:由方程组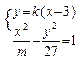 ,消去
,消去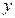 后得到形如
后得到形如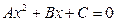 的方程。当
的方程。当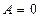 时,该方程有一解,当
时,该方程有一解,当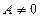 时,
时,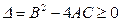 恒成立。假设该学生的演算过程是正确的,则实数m的取值范围是 ( )
恒成立。假设该学生的演算过程是正确的,则实数m的取值范围是 ( )
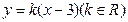 与双曲线
与双曲线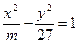 。某学生做了如下变形:由方程组
。某学生做了如下变形:由方程组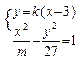 ,消去
,消去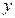 后得到形如
后得到形如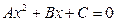 的方程。当
的方程。当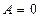 时,该方程有一解,当
时,该方程有一解,当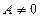 时,
时,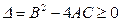 恒成立。假设该学生的演算过程是正确的,则实数m的取值范围是 ( )
恒成立。假设该学生的演算过程是正确的,则实数m的取值范围是 ( )A.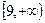 | B.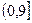 | C.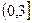 | D.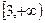 |
B
略

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
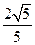 的椭圆的一个顶点是抛物线
的椭圆的一个顶点是抛物线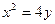 的焦点,过椭圆右焦点F的直线l交椭圆于A、B两点,交y轴于点M,且
的焦点,过椭圆右焦点F的直线l交椭圆于A、B两点,交y轴于点M,且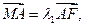
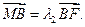
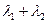 为定值。
为定值。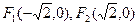 满足条件
满足条件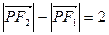 的点P的轨迹是曲线E,直线
的点P的轨迹是曲线E,直线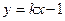 与曲线E交于A、B两点。
与曲线E交于A、B两点。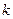 的取值范围;
的取值范围;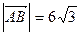 且曲线E上存在点C,使
且曲线E上存在点C,使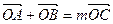 ,求
,求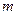 的值及点C的坐标.
的值及点C的坐标.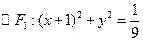 、
、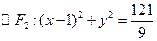 ,椭圆C的方程为
,椭圆C的方程为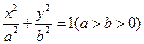 ,
,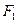 、
、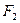 分别为椭圆C的两个焦点,设
分别为椭圆C的两个焦点,设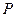 为椭圆C上一点,存在以
为椭圆C上一点,存在以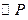 与
与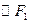 外切、与
外切、与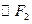 内切
内切
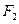 作斜率为
作斜率为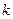 的直线与椭圆C相交于A、B两点,与
的直线与椭圆C相交于A、B两点,与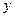 轴相交于点D,若
轴相交于点D,若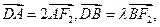 求
求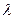 的值;
的值;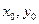 )在椭圆
)在椭圆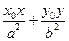 =1.”利用上述结论,解答下面问题:
=1.”利用上述结论,解答下面问题: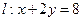 上的动点,过点Q作椭圆C的两条切线QM、QN,
上的动点,过点Q作椭圆C的两条切线QM、QN,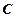 关于
关于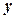 轴对称,它的顶点在坐标原点,并且经过点
轴对称,它的顶点在坐标原点,并且经过点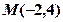 。
。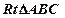 的三个顶点在抛物线
的三个顶点在抛物线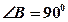 且点
且点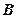 的横坐标为1,过点
的横坐标为1,过点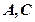 分别作抛物线
分别作抛物线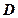 ,直线
,直线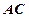 与
与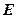 ,当直线
,当直线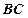 的斜率在
的斜率在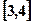 上变化时,直线
上变化时,直线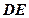 斜率是否存在最大值,若存在,求其最大值和直线
斜率是否存在最大值,若存在,求其最大值和直线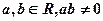 ,则直线
,则直线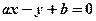 和曲线
和曲线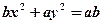 的大致图形可以是 ( )
的大致图形可以是 ( )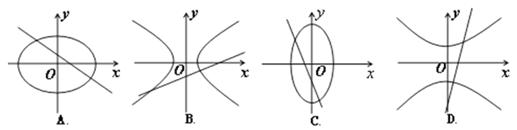
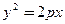 的焦点与椭圆
的焦点与椭圆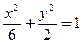 右焦点重合,则
右焦点重合,则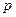 的值为( )
的值为( ) 与椭圆
与椭圆 有相同的焦点;
有相同的焦点; 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率; 为常数,若
为常数,若 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线; 的焦点作直线与抛物线相交于A、B两点,则使它们的横坐标之和
的焦点作直线与抛物线相交于A、B两点,则使它们的横坐标之和 ,则动点P的
,则动点P的