题目内容
(本小题满分13分)已知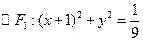 、
、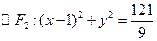 ,椭圆C的方程为
,椭圆C的方程为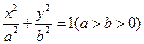 ,
,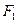 、
、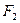 分别为椭圆C的两个焦点,设
分别为椭圆C的两个焦点,设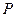 为椭圆C上一点,存在以
为椭圆C上一点,存在以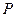 为圆心的
为圆心的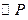 与
与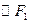 外切、与
外切、与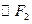 内切
内切
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点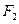 作斜率为
作斜率为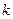 的直线与椭圆C相交于A、B两点,与
的直线与椭圆C相交于A、B两点,与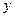 轴相交于点D,若
轴相交于点D,若
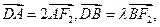 求
求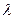 的值;
的值;
(Ⅲ)已知真命题:“如果点T(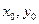 )在椭圆
)在椭圆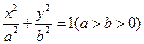 上,那么过点T
上,那么过点T
的椭圆的切线方程为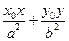 =1.”利用上述结论,解答下面问题:
=1.”利用上述结论,解答下面问题:
已知点Q是直线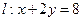 上的动点,过点Q作椭圆C的两条切线QM、QN,
上的动点,过点Q作椭圆C的两条切线QM、QN,
M、N为切点,问直线MN是否过定点?若是,请求出定点坐标;若不是,请说明理由。
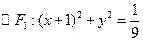 、
、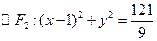 ,椭圆C的方程为
,椭圆C的方程为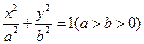 ,
,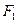 、
、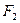 分别为椭圆C的两个焦点,设
分别为椭圆C的两个焦点,设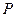 为椭圆C上一点,存在以
为椭圆C上一点,存在以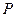 为圆心的
为圆心的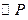 与
与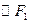 外切、与
外切、与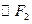 内切
内切
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点
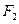 作斜率为
作斜率为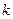 的直线与椭圆C相交于A、B两点,与
的直线与椭圆C相交于A、B两点,与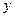 轴相交于点D,若
轴相交于点D,若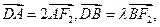 求
求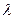 的值;
的值;(Ⅲ)已知真命题:“如果点T(
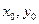 )在椭圆
)在椭圆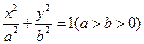 上,那么过点T
上,那么过点T的椭圆的切线方程为
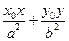 =1.”利用上述结论,解答下面问题:
=1.”利用上述结论,解答下面问题:已知点Q是直线
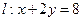 上的动点,过点Q作椭圆C的两条切线QM、QN,
上的动点,过点Q作椭圆C的两条切线QM、QN,M、N为切点,问直线MN是否过定点?若是,请求出定点坐标;若不是,请说明理由。
(Ⅰ)椭圆C的方程为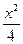 +
+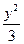 =1
=1
(Ⅱ)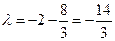
(Ⅲ)直线MN必过定点(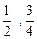 )
)
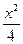 +
+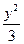 =1
=1(Ⅱ)
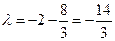
(Ⅲ)直线MN必过定点(
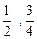 )
)本题主要考查直线、圆、椭圆等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想
(Ⅰ)依题意可知,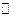 P与
P与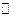
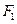 外切、
外切、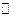
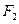 内切. 设
内切. 设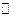 P的半径为
P的半径为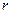 ,则
,则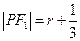
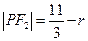 -----------------------------------2分
-----------------------------------2分
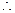
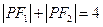 , 2
, 2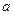 =4,2
=4,2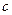 =
=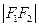 =2
=2
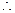
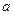 =2,c="1" , 椭圆C的方程为
=2,c="1" , 椭圆C的方程为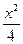 +
+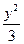 ="1 " -----------------------
="1 " ----------------------- -4分
-4分
(Ⅱ)直线AB:y=k(x-1),由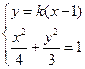
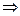
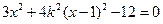
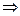
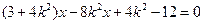 ,令A
,令A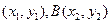 ,则
,则 ,
,
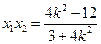 , ------------------------------------6分
, ------------------------------------6分
∵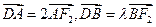
∴ ,
,
∵2=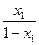 ,
, , ------------------------------------8分
, ------------------------------------8分
2+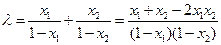
=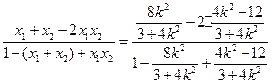
=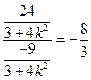 , ∴
, ∴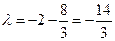 . -----------------------10分
. -----------------------10分
(Ⅲ)设Q(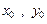 ),M(
),M(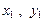 ),N(
),N(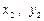 )
)
则切线QM: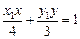
切线QN:
∴ ∴M、N在直线
∴M、N在直线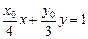 上
上
∴ 直线MN: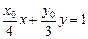 ------------------------------------12分
------------------------------------12分
又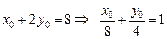
∴直线MN必过定点(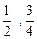 ). ------------------------------------13分
). ------------------------------------13分
(Ⅰ)依题意可知,
 P与
P与
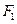 外切、
外切、
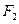 内切. 设
内切. 设 P的半径为
P的半径为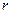 ,则
,则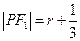
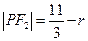 -----------------------------------2分
-----------------------------------2分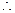
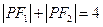 , 2
, 2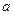 =4,2
=4,2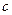 =
=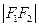 =2
=2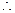
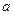 =2,c="1" , 椭圆C的方程为
=2,c="1" , 椭圆C的方程为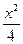 +
+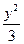 ="1 " -----------------------
="1 " ----------------------- -4分
-4分(Ⅱ)直线AB:y=k(x-1),由
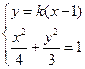
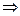
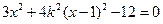
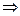
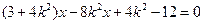 ,令A
,令A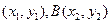 ,则
,则 ,
,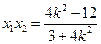 , ------------------------------------6分
, ------------------------------------6分∵
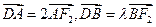
∴
 ,
,∵2=
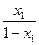 ,
, , ------------------------------------8分
, ------------------------------------8分2+
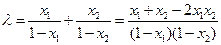
=
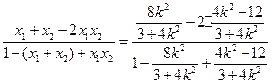
=
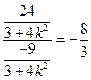 , ∴
, ∴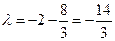 . -----------------------10分
. -----------------------10分(Ⅲ)设Q(
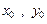 ),M(
),M(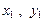 ),N(
),N(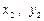 )
)则切线QM:
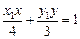
切线QN:

∴
 ∴M、N在直线
∴M、N在直线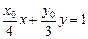 上
上∴ 直线MN:
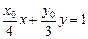 ------------------------------------12分
------------------------------------12分又
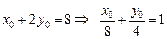
∴直线MN必过定点(
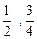 ). ------------------------------------13分
). ------------------------------------13分
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
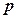 :“方程
:“方程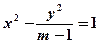 表示焦点在
表示焦点在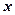 轴上的双曲线”,命题
轴上的双曲线”,命题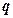 :“在区间
:“在区间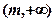 上,函数
上,函数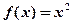 单调递增”,若
单调递增”,若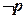 是真命题,
是真命题,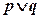 是真命题,求实数
是真命题,求实数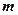 的取值范围。
的取值范围。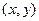 满足:
满足: ,求点P的轨迹方程。
,求点P的轨迹方程。 是圆
是圆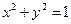 上的一个动点,过点
上的一个动点,过点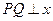 轴于点
轴于点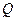 ,设
,设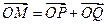 ,则点
,则点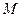 的轨迹方程______________;
的轨迹方程______________;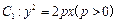 的焦点
的焦点 恰好是曲线
恰好是曲线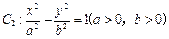 的右焦点,且
的右焦点,且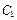 与
与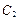 交点的连线过点
交点的连线过点
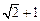

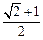
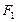 ,
,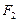 分别是双曲线
分别是双曲线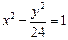 的左、右焦点,
的左、右焦点,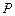 是双曲线上的一点,若
是双曲线上的一点,若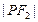 ,
,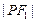 ,
,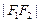 构成公差为正数的等差数列,则
构成公差为正数的等差数列,则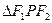 的面积为
的面积为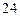
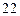
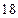
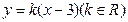 与双曲线
与双曲线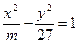 。某学生做了如下变形:由方程组
。某学生做了如下变形:由方程组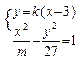 ,消去
,消去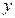 后得到形如
后得到形如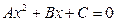 的方程。当
的方程。当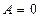 时,该方程有一解,当
时,该方程有一解,当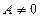 时,
时,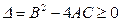 恒成立。假设该学生的演算过程是正确的,则实数m的取值范围是 ( )
恒成立。假设该学生的演算过程是正确的,则实数m的取值范围是 ( )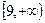
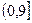
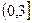
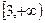
 的左
的左 、右焦点为F1、F2,其一条渐近线为y=x,点P
、右焦点为F1、F2,其一条渐近线为y=x,点P 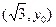 在该双曲线上,则
在该双曲线上,则 =( )
=( )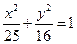 的焦点为
的焦点为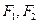 ,过F2垂直于x轴的直线交椭圆于一点P,那么|PF1|的值是 。
,过F2垂直于x轴的直线交椭圆于一点P,那么|PF1|的值是 。