题目内容
【题目】在某企业中随机抽取了5名员工测试他们的艺术爱好指数
和创新灵感指数
，统计结果如下表（注：指数值越高素质越优秀）：
（1）求创新灵感指数
关于艺术爱好指数
的线性回归方程；
（2）企业为提高员工的艺术爱好指数，要求员工选择音乐和绘画中的一种进行培训，培训音乐次数
对艺术爱好指数的提高量为
，培训绘画次数对艺术爱好指数的提高量为
，其中
为参加培训的某员工已达到的艺术爱好指数.艺术爱好指数已达到3的员工甲选择参加音乐培训，艺术爱好指数已达到4的员工乙选择参加绘画培训，在他们都培训了20次后，估计谁的创新灵感指数更高？
参考公式：回归方程
中，
，
.
参考数据：
，
【答案】（1）
（2）培训后乙的创新灵感指数更高
【解析】
（1）先求得
，再根据提供的数据，求得
，写出回归直线方程.
（2）根据培训音乐次数
对艺术爱好指数
的提高量为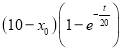
，培训绘画次数对艺术爱好指数的提高量为
，分别得到员工甲经过20次的培训后，他们的艺术爱好指数，再估计他们的创新灵感指数，比较即可.
（1）设
，有
，
，
.
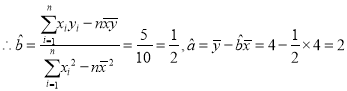（2）员工甲经过20次的培训后，
估计他的艺术爱好指数将达到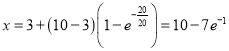
，
因此估计他的创新灵感指数为
.
员工乙经过20次的培训后，
估计他的艺术爱好指数将达到
，
因此估计他的创新灵感指数为
.
由于
，故培训后乙的创新灵感指数更高.
【题目】已知函数
的定义域为[-1,5]，部分对应值如下表， 
的导函数
的图象如图所示，下列关于
的命题：
| -1 | 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
①函数
的极大值点为0,4；
②函数
在[0,2]上是减函数；
③如果当
时， 
的最大值是2，那么t的最大值为4；
④当1<a<2时，函数
有4个零点.
其中正确命题的序号是__________．
【题目】某市十所重点中学进行高三联考，共有5000名考生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：
分组 | 频数 | 频率 |
| ① | ② |
|
| |
|
| |
| 36 |
|
|
| |
| 12 | ③ |
|
| |
合计 | ④ |
（1）根据上面频率分布表，推出①，②，③，④处的数值分别为 ， ， ， ；
（2）在所给的坐标系中画出区间
上的频率分布直方图；
（3）根据题中信息估计总体：
（i）120分及以上的学生数；
（ii）平均分；
（iii）成绩落在
中的概率.
【题目】10月1日，某品牌的两款最新手机（记为
型号，
型号）同时投放市场，手机厂商为了解这两款手机的销售情况，在10月1日当天，随机调查了5个手机店中这两款手机的销量（单位：部），得到下表：
手机店 |
|
|
|
|
|
| 6 | 6 | 13 | 8 | 11 |
| 12 | 9 | 13 | 6 | 4 |
（Ⅰ）若在10月1日当天，从
，
这两个手机店售出的新款手机中各随机抽取1部，求抽取的2部手机中至少有一部为型号手机的概率；
（Ⅱ）现从这5个手机店中任选3个举行促销活动，用型号手机销量超过型号手机销量的手机店的个数，求随机变量
的分布列和数学期望；
（III）经测算，型号手机的销售成本
（百元）与销量（部）满足关系
.若表中型号手机销量的方差
，试给出表中5个手机店的型号手机销售成本的方差
的值.（用
表示，结论不要求证明）
