题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的点.
上的点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知斜率存在又不经过原点的直线![]() 与圆
与圆![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() 两点.探究:在椭圆
两点.探究:在椭圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,请求出实数
,若存在,请求出实数![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
【答案】(1)![]() (2)存在,
(2)存在,![]()
【解析】
(1)根据题意列方程组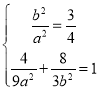 , 求解即可.
, 求解即可.
(2)假设在椭圆![]() 上存在点
上存在点![]() ,使得
,使得![]() .设直线
.设直线![]() ,圆心
,圆心![]() 到直线
到直线![]() 的距离等于半径1,可知
的距离等于半径1,可知![]() ,整理的
,整理的![]() ,直线
,直线![]() 与椭圆联立得,
与椭圆联立得,![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,根据
,根据![]() ,表示出点
,表示出点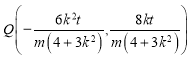 ,代入椭圆得
,代入椭圆得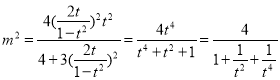 ,求解即可.
,求解即可.
(1)依题意,![]() ,故
,故![]() ①.
①.
将![]() 代入椭圆的方程中,可得
代入椭圆的方程中,可得![]() ②.
②.
联立①②,解得![]()
故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)假设在椭圆![]() 上存在点
上存在点![]() ,使得
,使得![]() .
.
依题意,设直线![]() ,
,
因为直线![]() 与圆
与圆![]() 相切,
相切,
所以圆心![]() 到直线
到直线![]() 的距离等于半径
的距离等于半径![]() ,即
,即![]()
整理得![]() .
.
当![]() 时,不合题意,舍去;
时,不合题意,舍去;
当![]() 且
且![]() 时,得
时,得![]() ,把
,把![]() 代入椭圆
代入椭圆![]()
的方程![]() 得:
得:![]() .
.
易知,圆在椭圆内,所以直线![]() 与椭圆
与椭圆![]() 相交,设
相交,设![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
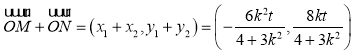 .
.
因为![]() ,故
,故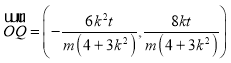 ,
,
即![]() 的坐标为
的坐标为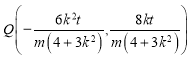 .
.
又因为![]() 在椭圆上,所以
在椭圆上,所以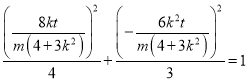 ,
,
得![]() .
.
把![]() 代入得
代入得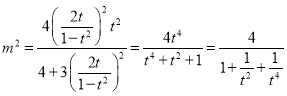 ;
;
因为![]() ,所以
,所以![]() ,
,![]() ,
,
即![]() 或
或![]() ,
,
综上所述实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某学校为更好进行校纪、校风管理,争创文明学校,由志愿者组成“小红帽”监督岗,对全校的不文明行为进行监督管理,对有不文明行为者进行批评教育,并作详细的登记,以便跟踪调查下表是![]() 个周内不文明行为人次统计数据:
个周内不文明行为人次统计数据:
周次 |
|
|
|
|
|
不文明行为人次 |
|
|
|
|
|
(1)请利用所给数据求不文明人次![]() 与周次
与周次![]() 之间的回归直线方程
之间的回归直线方程![]() ,并预测该学校第
,并预测该学校第![]() 周的不文明人次;
周的不文明人次;
(2)从第![]() 周到第
周到第![]() 周记录得知,高一年级有
周记录得知,高一年级有![]() 位同学,高二年级有
位同学,高二年级有![]() 位同学已经有
位同学已经有![]() 次不文明行为.学校德育处决定先从这
次不文明行为.学校德育处决定先从这![]() 人中任选
人中任选![]() 人进行重点教育,求抽到的两人恰好来自同一年级的概率
人进行重点教育,求抽到的两人恰好来自同一年级的概率
参考公式: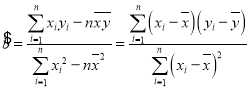 ,
,![]()