Question

【题目】已知函数f（x）＝ex﹣2mx﹣n（0＜x＜1），其中m，n∈R，e为自然对数的底数.

（1）试讨论函数f（x）的极值；

（2）记函数g（x）＝ex﹣mx2﹣nx﹣1（0＜x＜1），且g（x）的图象在点处的切的斜率为，若函数g（x）存在零点，试求实数m的取值范围.

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）求导后对的取值分类，注意在定义域内，得函数有无极值，且求出极值；

（2）求导得到等于，求出在处的导数值，既是在处的切线的斜率，由题意得的关系，然后讨论的范围使存在零点，进而求出的范围．

(1) ，①当2m≤1时，即时，1exe，∴ ，f(x)在(0，1)上单调递增，f(x)无极值；

②当2m≥e时，即时， ，f(x)在(0，1)上单调递减，f(x)无极值；

③当<e时，，x＝ln2e，当时，f(x)0，f(x)单调递减，

当1xln2e时，，函数f(x)单调递增，所以(0，1)上函数f(x)有极大值，无极小值，且极大值为f(ln2e)＝2e﹣2mln2e﹣n；

综上：当或，函数f(x)无极值；

当<e时，f(x)的极小值为2m﹣2mln2m﹣n，无极大值；

(2)由题意得：g'(x)＝ex﹣2mx﹣n，

g(x)的图象在点处的切线的斜率为1﹣，

而g'﹣n，所以m+n＝e﹣1，

∴n＝e﹣1﹣m，g(x)＝ex﹣mx2﹣(e﹣m﹣1)x﹣1，

所以g(0)＝0，g(1)＝e﹣m﹣(e﹣m﹣1)﹣1＝0，

设x0为g(x)在区间(0，1)内的零点，则g(0)g(x0)＝0，

可知g(x)在区间(0，x0)内不可能单调递增，也不可能单调递减，

故g'(x)不可能恒为正，也不可能恒为负，故g(x)在(0，x0)内存在零点x1，在区间(x0，1)内存在零点x2，所以g'(x)＝f(x)在区间(0，1)内至少有两个零点，

由(1)知当时，g'(x)在区间(0，1)单调递增，

故g'(x)在区间(0，1)内至多有一个零点；

当时，g'(x)在区间(0，ln2m)内单调递减，(ln2m，1)内单调递增，

所以x1∈0，ln2m)，x2∈(ln2m，1)，

则g'(0)＝1﹣(e﹣m﹣1)0，g'(1)＝e﹣2m﹣(e﹣m﹣1)0，

g'(ln2m)＝2m﹣2mln2m﹣n＝3m﹣2mln2m+1﹣e0，

令h(x)﹣xlnx+1﹣e，()，

则h'(x)，令h'(x)＝0，则得，

当1时，h'(x) ，g(x)单调递增，

当时，h'(x)0，h(x)单调递减，

所以h(x)最大值＝h(1﹣；所以g'(ln2m)0恒成立，

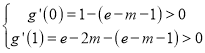由得，

综上，实数m的取值范围(e﹣2，1)