题目内容
15.命题“?x0∈R,使得x02+x0+1≤0”的否定为(( )| A. | ?x∈R,都有x2+x+1≤0 | B. | ?x0∈R,使得x02+x0+1≥0 | ||
| C. | ?x∈R,都有x2+x+1>0 | D. | ?x0∈R,使得x02+x0+1>0 |
分析 直接利用特称命题的否定是全称命题,写出经过即可.
解答 解:因为特称命题的否定是全称命题,所以,命题“?x0∈R,使得x02+x0+1≤0”的否定为:?x∈R,都有x2+x+1>0.
故选:C.
点评 本题考查命题的否定,特称命题与全称命题的否定关系,基本知识的考查.

练习册系列答案
相关题目
5.已知数列{an}是以a为首项,q为公比的等比数列,Sn为它的前n项和.
(1)当S1,S3,S4成等差数列时,求q的值;
(2)若bn=anan+1(n∈N+),试求数列{bn}的前n项和Sn的公式.
(1)当S1,S3,S4成等差数列时,求q的值;
(2)若bn=anan+1(n∈N+),试求数列{bn}的前n项和Sn的公式.
20.已知函数f(x)的部分图象如图,则f(x)的解析式可能为( )
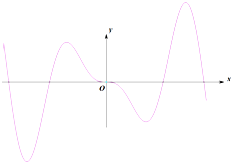

| A. | f(x)=xcosx-sinx | B. | f(x)=xsinx | C. | f(x)=xcosx+sinx | D. | f(x)=xcosx |
18.用反证法证明命题“若a+b=1,则a,b至少有一个不比1大时,”首先假设( )
| A. | a,b都小于等于1 | B. | a,b都大于1 | ||
| C. | a,b都大于等于1 | D. | a,b都小于1当a<0时 |
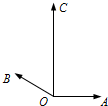 如图,平面内有三个向量$\overrightarrow{OA},\;\overrightarrow{OB},\;\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为150°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为90°,且$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$,$|{\overrightarrow{OC}}|=2$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}\;(λ,μ∈R)$,则λ+μ=( )
如图,平面内有三个向量$\overrightarrow{OA},\;\overrightarrow{OB},\;\overrightarrow{OC}$,其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为150°,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为90°,且$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$,$|{\overrightarrow{OC}}|=2$,若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}\;(λ,μ∈R)$,则λ+μ=( )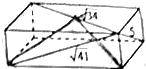 如图,已知长方体过一个顶点的三条面对角线的长分别为5,$\sqrt{34}$,$\sqrt{41}$,则其外接球(长方体的顶点均在球面上)的表面积是50π.
如图,已知长方体过一个顶点的三条面对角线的长分别为5,$\sqrt{34}$,$\sqrt{41}$,则其外接球(长方体的顶点均在球面上)的表面积是50π.