题目内容
19．
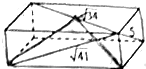如图，已知长方体过一个顶点的三条面对角线的长分别为5，$\sqrt{34}$，$\sqrt{41}$，则其外接球（长方体的顶点均在球面上）的表面积是50π．
分析 先求出长方体的棱长，再求出它的体对角线即求出外接球的直径，由此据公式即可球的表面积，本题采用了设而不求的技巧，没有解棱的长度，直接整体代换求出了体对角线的长度．
解答 解：长方体一顶点出发的三条棱长的长分别为a，b，c，
则a2+b2=25，b2+c2=34，c2+a2=41，
得a2+b2+c2=50．
于是，球的直径2R满足4R2=（2R）2=a2+b2+c2=50．
故外接球的表面积为S=4πR2=50π．
故答案为：50π．
点评 本题考查长方体的几何性质，长方体与其外接球的关系，以及球的表面积公式，训练了空间想象能．．
练习册系列答案
阅读快车系列答案
相关题目
15．命题“?x0∈R，使得x02+x0+1≤0”的否定为（（ ）
| A． | ?x∈R，都有x2+x+1≤0 | B． | ?x0∈R，使得x02+x0+1≥0 | ||
| C． | ?x∈R，都有x2+x+1＞0 | D． | ?x0∈R，使得x02+x0+1＞0 |