题目内容
若直线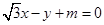 与圆
与圆 相切, 则实数m等于
相切, 则实数m等于
A. 或 或 | B. 或 或 |
C. 或 或 | D. 或 或 |
C
解析试题分析:因为将圆 化为标准式,配方可知圆的方程(x-1)2+y2=3,然后根据直线与圆相切,则说明圆心(1,0)到直线的距离等于半径
化为标准式,配方可知圆的方程(x-1)2+y2=3,然后根据直线与圆相切,则说明圆心(1,0)到直线的距离等于半径
d= ,进而解得实数m等于.
,进而解得实数m等于. 或
或 ,选C.
,选C.
考点:本题主要考查了直线和圆的位置关系,是基础题.
点评:解决该试题的关键是求解圆心到直线的距离,或者利用联立方程组得到方程中判别式等于零,求解参数m的值。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
已知两点 ,点
,点 是圆
是圆 上任意一点,则
上任意一点,则 面积的最小值是( ).
面积的最小值是( ).
A. | B. | C. | D. |
直线 与椭圆
与椭圆 交于
交于 两点,以线段
两点,以线段 为直径的圆过椭圆的右焦点,则椭圆
为直径的圆过椭圆的右焦点,则椭圆 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
若圆C与圆(x+2)2+(y-1)2=1关于原点对称,则圆C的方程是( )
| A.(x-2)2+(y+1)2=1 | B.(x-2)2+(y-1)2=1 |
| C.(x-1)2+(y+2)2=1 | D.(x+1)2+(y-2)2=1 |
设A,B为直线 与圆
与圆 的两个交点,则|AB|=( )
的两个交点,则|AB|=( )
| A.1 | B. | C. | D.2 |
点 与圆
与圆 上任一点连线的中点轨迹方程是( )
上任一点连线的中点轨迹方程是( )
A. | B. |
C. | D. |
直线 按向量
按向量 平移后与圆
平移后与圆 相切,则
相切,则 的值等于( )
的值等于( )
A.8或 | B.6或 | C.4或 | D.2或 |
由直线 上的一点向圆
上的一点向圆 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )
| A.1 | B. | C.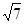 | D.3 |
直线 与圆
与圆 的位置关系为 ( )
的位置关系为 ( )
| A.相切 | B.相交但直线不过圆心 |
| C.直线过圆心 | D.相离 |