题目内容
设A,B为直线 与圆
与圆 的两个交点,则|AB|=( )
的两个交点,则|AB|=( )
| A.1 | B. | C. | D.2 |
D
解析试题分析:显然直线过圆的圆心,所以|AB|长即为直径的长度,所以|AB|="2."
考点:本小题主要考查直线与圆相交的弦长的计算.
点评:解决本题关键是发现直线过圆心,所以弦长等于直径长.

练习册系列答案
相关题目
过点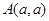 可作圆
可作圆 的两条切线,则实数
的两条切线,则实数 的取值范围为( )
的取值范围为( )
A. 或 或 | B.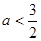 |
C. 或 或 | D. 或 或 |
若直线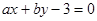 和圆
和圆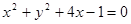 相切与点
相切与点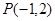 ,则
,则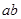 的值为( )
的值为( )
A.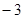 | B.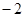 | C. | D.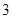 |
已知Rt△ABC的两条直角边长分别为a、b,斜边长为c,则直线ax+by+c=0与圆x2+y2=1的位置关系是( )
| A.相交 | B.相切 | C.相离 | D.相切或相交 |
已知圆心为C(6,5),且过点B(3,6)的圆的方程为
A.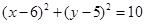 | B. |
C. | D. |
若直线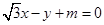 与圆
与圆 相切, 则实数m等于
相切, 则实数m等于
A. 或 或 | B. 或 或 |
C. 或 或 | D. 或 或 |
已知 ,点
,点
 是圆
是圆 内一点,直线
内一点,直线 是以点
是以点 为中点的弦所在的直线,直线
为中点的弦所在的直线,直线 的方程是
的方程是 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. ,且 ,且 与圆相交 与圆相交 | B. ,且 ,且 与圆相切 与圆相切 |
C. ,且 ,且 与圆相离 与圆相离 | D. ,且 ,且 与圆相离 与圆相离 |
圆 的圆心到直线
的圆心到直线 的距离是 ( )
的距离是 ( )
A. | B. | C. | D. |
三角形 ,顶点
,顶点 ,该三角形的内切圆方程为( )
,该三角形的内切圆方程为( )
A. | B.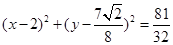 |
C. | D. |