Question

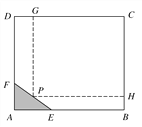
【题目】如图所示，为了保护环境，实现城市绿化，某房地产公司要在拆迁地长方形ABCD处规划一块长方形地面HPGC，建造住宅小区公园，但不能越过文物保护区三角形AEF的边线EF.已知AB＝CD＝200 m，BC＝AD＝160 m，AF＝40 m，AE＝60 m，问如何设计才能使公园占地面积最大，求出最大面积．

Answer 1

【答案】详见解析.

【解析】试题分析: 在EF上取一点P，作PH⊥BC，PG⊥CD，垂足分别为H、G，设PH＝x，则140≤x≤200.

由三角形相似得出PG用x表示,进而得出公园占地面积关于x的函数,用配方法得出函数的最值,以及取到最值时的x值.

试题解析:

如题图，在EF上取一点P，作PH⊥BC，PG⊥CD，垂足分别为H、G，设PH＝x，则140≤x≤200.

由三角形相似性质PG＝120＋ (200－x)，

∴公园占地面积为S＝x[120＋ (200－x)]

＝－x2＋x

＝－ (x－190)2＋×1902(140≤x≤200)，

∴当x＝190时，Smax＝m2.

答：在EF上取一点P，使P到BC距离为190m时，公园PHCG占地面积最大，最大面积为m2.

点睛: 本题考查函数的实际应用问题,解决问题的关键是利用相似求出函数的解析式,用二次函数的单调性解决函数的最值.解决函数模型应用的解答题，还有以下几点容易造成失分：①读不懂实际背景，不能将实际问题转化为函数模型．②对涉及的相关公式，记忆错误．③在求解的过程中计算错误.