题目内容
【题目】(本题满分12分)已知![]()
(1)求函数![]() 的单调区间;
的单调区间;
(2)设![]() ,若存在
,若存在![]() 使得
使得![]() 成立,求
成立,求![]() 的取值范围。
的取值范围。
【答案】(1) 当![]() ,
,![]() 在单调递增区间为
在单调递增区间为![]() ;
;![]() 时,
时,![]() 的递增区间为
的递增区间为![]() ,递减区间为
,递减区间为![]() ;(2) [0,+∞).
;(2) [0,+∞).
【解析】试题分析:(1)含参讨论研究函数的单调性;(2)存在![]() 使得
使得![]() 成立,即求函数的最大值大于等于零即可,也可以变量分离求最值.
成立,即求函数的最大值大于等于零即可,也可以变量分离求最值.
试题解析:
(1) 函数的定义域为![]()
![]()
若![]() ,
,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增。
上单调递增。
若![]() ,令
,令![]() ,解得
,解得![]() ,
,
令![]() ,解得
,解得![]()
综上,当![]() ,
,![]() 在单调递增区间为
在单调递增区间为![]() ;
;
![]() 时,
时,![]() 的递增区间为
的递增区间为![]() ,递减区间为
,递减区间为![]() 。
。
(2)当b=1时,f(x)=ln x-x+a+1(x>0).
原题即为存在x使得ln x-x+a+1≥0,
∴a≥-ln x+x-1,
令g(x)=-ln x+x-1,
则g′(x)=-![]() +1=
+1=![]() .令g′(x)=0,解得x=1.
.令g′(x)=0,解得x=1.
∵当0<x<1时,g′(x)<0,∴g(x)为减函数,
当x>1时,g′(x)>0,∴g(x)为增函数,
∴g(x)min=g(1)=0.
∴a≥g(1)=0.∴a的取值范围为[0,+∞).

【题目】微信红包是一款可以实现收发红包、查收记录和提现的手机应用.某网络运营商对甲、乙两个品牌各5种型号的手机在相同环境下抢到的红包个数进行统计,得到如下数据:
手机品牌 型号 | I | II | III | IV | V |
甲品牌(个) | 4 | 3 | 8 | 6 | 12 |
乙品牌(乙) | 5 | 7 | 9 | 4 | 3 |
手机品牌 红包个数 | 优 | 非优 | 合计 |
甲品牌(个) | |||
乙品牌(个) | |||
合计 |
(1)如果抢到红包个数超过5个的手机型号为“优”,否则为“非优”,请完成上述2×2列联表,据此判断是否有85%的把握认为抢到的红包个数与手机品牌有关?
(2)如果不考虑其他因素,要从甲品牌的5种型号中选出3种型号的手机进行大规模宣传销售.
①求在型号I被选中的条件下,型号II也被选中的概率;
②以![]() 表示选中的手机型号中抢到的红包超过5个的型号种数,求随机变量
表示选中的手机型号中抢到的红包超过5个的型号种数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
下面临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: 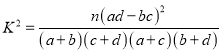 ,其中
,其中![]() .
.