题目内容
【题目】通过研究学生的学习行为,专家发现,学生的注意力着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设f(t)表示学生注意力随时间t(分钟)的变化规律\left(f(t)越大,表明学生注意力越集中),经过实验分析得知: 
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,教师能否在学生达到所需的状态下讲授完这道题目?
【答案】(1)讲课开始10分钟,学生的注意力最集中,能持续10分钟;(2)讲课开始25分钟时,学生的注意力比讲课开始后5分钟更集中;(3)经过适当安排,老师可以在学生达到所需要的状态下讲授完这道题.
【解析】试题分析:应用问题首先要认真细致的读题审题,本题为分段函数问题,根据分段函数问题分段处理原则,针对每一段函数根据相应的定义域要求,求出每一段的最大值,再比较得出最大值;比较两个函数值的大小,按两个自变量的大小,分别对号入座,求出相应的函数值后,再比较大小;分段函数解不等式问题,在每段的定义域下分别解不等式,再取三段的解集的并集.
试题解析:
(1)当0<t10时,f(t)=t2+24t+100
=(t12)2+244是增函数,且f(10)=240;
当20<t40时,f(t)=7t+380是减函数,
且f(20)=240.
所以,讲课开始10分钟,学生的注意力最集中,能持续10分钟。
(2)f(5)=195,f(25)=205,
故讲课开始25分钟时,学生的注意力比讲课开始后5分钟更集中。
(3)当0<t10时,f(t)=t2+24t+100=180,则t=4;
当20<t40时,令f(t)=7t+380=180,
t≈28.57,则学生注意力在180以上所持续的时间
28.574=24.57>24,
所以,经过适当安排,老师可以在学生达到所需要的状态下讲授完这道题。
【点精】应用问题首先要认真细致的审题,逐字逐句的读题,把实际问题转化为数学问题.本题为分段函数问题,根据分段函数问题分段处理原则,分段函数涉及到定义域、值域、单调性、奇偶性、最值、解方程和解不等式诸多问题,分段函数的定义域为各段定义域的并集,求最值时,针对每一段函数根据相应的定义域要求,求出每一段的极大值,再比较得出最大值;比较两个函数值的大小,按两个自变量的大小,分别对号入座,求出相应的函数值后,再比较大小;分段函数解不等式问题,在每段的定义域下分别解不等式,再取三段的解集的并集;

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案【题目】某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.
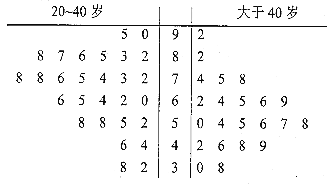
(1)根据茎叶图中的数据完成![]() 列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
购买意愿强 | 购买意愿弱 | 合计 | |
20~40岁 | |||
大于40岁 | |||
合计 |
(2)从购买意愿弱的市民中按年龄进行分层抽样,共抽取5人,从这5人中随机抽取2人进行采访,记抽到的2人中年龄大于40岁的市民人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() .
.