题目内容
2.(重点中学做)已知函数f(x)=$\frac{(x+1)lnx}{x-1}$,g(x)=-2x3-3x2+2.(1)讨论函数f(x)的单调性;
(2)证明:对任意x1∈(0,1)∪(1,+∞),总存在x2∈(-∞,0),使得f(x1)>g(x2)成立.
分析 (1)求导数,$f′(x)=\frac{-2lnx+x-\frac{1}{x}}{(x-1)^{2}}$,想法判断f′(x)的符号,从而可设$h(x)=-2lnx+x-\frac{1}{x}$,再求导数,$h′(x)=\frac{(x-1)^{2}}{{x}^{2}}$,显然h′(x)≥0,从而可得出h(x)在(0,+∞)为增函数,并且h(1)=0,从而可判断出f′(x)在(0,1),(1,+∞)上的符号,从而得出f(x)的单调性;
(2)根据题意,可将问题转化为证明任意的x∈(0,1)∪(1,+∞)时,f(x)>g(x)min,这样便来求g(x)的最小值,根据导数符号容易判断出g(x)的最小值为1.从而来证明$\frac{(x+1)lnx}{x-1}>1$恒成立,从而可证明$\frac{x+1}{x-1}(lnx+\frac{2}{x+1}-1)>0$恒成立,可设r(x)=$lnx+\frac{2}{x+1}-1$,通过求导数,便可证明r(x)在(0,+∞)上单调递增,并且r(1)=0,这样根据r(x)的单调性即可判断r(x)在(0,1)和(1,+∞)上的符号,从而得出$\frac{x+1}{x-1}(lnx+\frac{2}{x+1}-1)>0$恒成立即可.
解答 解:(1)$f′(x)=\frac{-2lnx+x-\frac{1}{x}}{(x-1)^{2}}$,令h(x)=$-2lnx+x-\frac{1}{x}$,则:
$h′(x)=-\frac{2}{x}+1+\frac{1}{{x}^{2}}=\frac{(x-1)^{2}}{{x}^{2}}≥0$;
∴h(x)在(0,+∞)上单调递增;
∴x∈(0,1)时,h(x)<h(1)=0,f′(x)<0,∴f(x)在(0,1)上单调递减;
x∈(1,+∞)时,h(x)>h(1)=0,f′(x)>0,∴f(x)在(1,+∞)上单调递增;
即f(x)在(0,1)上单调递减,在(1,+∞)上单调递增;
(2)证明:g′(x)=-6x2-6x=-6x(x+1);
∴x∈(-∞,-1)时,g′(x)<0,x∈(-1,0)时,g′(x)>0;
∴g(-1)=1是g(x)的最小值;
∴问题等价于对任意的x∈(0,1)∪(1,+∞),f(x)>1恒成立;
即证$\frac{(x+1)lnx}{x-1}>1$恒成立;
也就是证$\frac{x+1}{x-1}(lnx+\frac{2}{x+1}-1)>0$恒成立;
设$r(x)=lnx+\frac{2}{x+1}-1$,$r′(x)=\frac{{x}^{2}+1}{x(x+1)^{2}}$>0;
∴r(x)在(0,+∞)上单调递增,r(1)=0;
∴x∈(0,1)时,r(x)<0,则$\frac{x+1}{x-1}(lnx+\frac{2}{x+1}-1)>0$;
x∈(1,+∞)时,r(x)>0,则$\frac{x+1}{x-1}(lnx+\frac{2}{x+1}-1)>0$;
综上可得:对任意的x1∈(0,1)∪(1,+∞),总存在x2∈(0,+∞),使得f(x1)>g(x2).
点评 考查根据函数导数符号判断函数的单调性的方法,函数的单调性定义的运用,根据导数符号求函数最小值的方法,将问题转化为与之等价的问题的方法.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案| A. | 3 | B. | 5 | C. | 2$\sqrt{5}$-1 | D. | 2$\sqrt{5}$+1 |
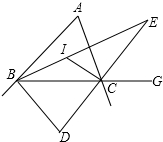 好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决,如图,在ABC中,∠BAC=50°,点I是两角B、C平分线的交点.
好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决,如图,在ABC中,∠BAC=50°,点I是两角B、C平分线的交点.