题目内容
【题目】一个盒子中装有大量形状大小一样但重量不尽相同的小球，从中随机抽取50个作为样本，称出它们的重量（单位：克），重量分组区间为[5，15]，(15，25]，(25，35]，(35，45]，由此得到样本的重量频率分布直方图（如图）．
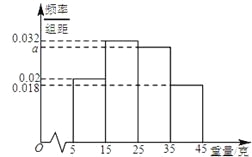
（1）求
的值；
（2）从盒子中随机抽取3个小球，其中重量在[5,15]内的小球个数为X，求X的分布列和数学期望. (以直方图中的频率作为概率).
【答案】（1）
；（2）分布列见解析，期望为
．
【解析】试题分析：（1）由频率分布直方图知，所有小矩形面积（频率）之和为1，可求得
；（2）由统计的知识，可知小球重量在
内的概率为
，因此随机变量
，利用二项分布概率公式可计算出所有概率，从而得概率分布表，再由期望公式可计算期望．
试题解析：（1）由题意，得
，解得；
（2）利用样本估计总体，该盒子中小球重量在
内的概率为
，
则.
的可能取值为
、
、
、
，
，
，
，
.
的分布列为：
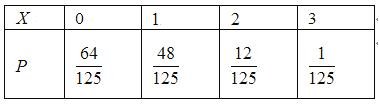
.（或者
）．
练习册系列答案
相关题目
【题目】某种植基地将编号分别为1，2，3，4，5，6的六个不同品种的马铃薯种在如图所示的
A | B | C | D | E | F |
这六块实验田上进行对比试验，要求这六块实验田分别种植不同品种的马铃薯，若种植时要求编号1，3，5的三个品种的马铃薯中至少有两个相邻，且2号品种的马铃薯不能种植在A、F这两块实验田上，则不同的种植方法有 ( )
A. 360种 B. 432种 C. 456种 D. 480种
