题目内容
【题目】已知二次函数f（x）=ax2+bx，g（x）=2x﹣1．
（1）当a=1时，若函数f（x）的图象恒在函数g（x）的图象上方，试求实数b 的取值范围；
（2）若y=f（x）对任意的x∈R均有f（x﹣2）=f（﹣x）成立，且f（x）的图象经过 点A（1， 
）．
①求函数y=f（x）的解析式；
②若对任意x＜﹣3，都有2k 
＜g（x）成立，试求实数k的最小值．
【答案】
（1）解：a=1时，若函数f（x）的图象恒在函数g（x）的图象上方，
则x2+bx＞2x﹣1，即x2+（b﹣2）x+1＞0恒成立，
即△=（b﹣2）2﹣4＜0，
解得：b∈（0，4）
（2）解：①若y=f（x）对任意的x∈R均有f（x﹣2）=f（﹣x）成立，且f（x）的图象经过点A（1， 
）．
则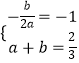 
，解得： 
，
∴y=f（x）= 
x2+ 
x，
②若对任意x＜﹣3，都有2k 
＜g（x）成立，
则对任意x＜﹣3，都有2k（ x+ ）＜2x﹣1成立，
则对任意x＜﹣3，都有k＞ 
= 
﹣ 
成立，
由x＜﹣3时， ﹣ ∈（ ， 
），
∴k≥ ，
故实数k的最小值为
【解析】（1）当a=1时，若函数f（x）的图象恒在函数g（x）的图象上方，则x2+bx＞2x﹣1，即x2+（b﹣2）x+1＞0恒成立，即△=（b﹣2）2﹣4＜0，解得实数b 的取值范围；（2）①若y=f（x）对任意的x∈R均有f（x﹣2）=f（﹣x）成立，且f（x）的图象经过 点A（1， ）．则 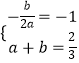，解得：a，b的值，可得函数y=f（x）的解析式；②若对任意x＜﹣3，都有2k ＜g（x）成立，则对任意x＜﹣3，都有k＞ = ﹣ 成立，进而可得实数k的最小值．
【考点精析】本题主要考查了二次函数的性质的相关知识点，需要掌握当
时，抛物线开口向上，函数在
上递减，在
上递增；当
时，抛物线开口向下，函数在上递增，在上递减才能正确解答此题．
