题目内容
【题目】设函数f(x)=xln(x﹣1)﹣a(x﹣2). (Ⅰ)若a=2017,求曲线f(x)在x=2处的切线方程;
(Ⅱ)若当x≥2时,f(x)≥0,求a的取值范围.
【答案】解:(Ⅰ)a=2017时,f(x)=xln(x﹣1)﹣2017(x﹣2), 则f′(x)=ln(x﹣1)+ ![]() ﹣2017,故f′(2)=﹣2015,
﹣2017,故f′(2)=﹣2015,
又f(2)=0,
故切线方程是:y﹣0=﹣2015(x﹣2),
即2015x+y﹣4030=0;
(Ⅱ)由f(x)≥0得xln(x﹣1)﹣a(x﹣2)≥0,而x≥2,
故ln(x﹣1)﹣ ![]() ≥0,
≥0,
设函数g(x)=ln(x﹣1)﹣ ![]() ,(x≥2),
,(x≥2),
于是问题转化为g(x)≥0对任意的x≥2恒成立,
注意到g(2)=0,故若g′(x)≥0,则g(x)递增,
从而g(x)≥g(2)=0,而g′(x)= ![]() ,
,
∴g′(x)≥0等价于x2﹣2a(x﹣1)≥0,
分离参数得a≤ 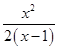 =
= ![]() [(x﹣1)+
[(x﹣1)+ ![]() +2],
+2],
由均值不等式得 ![]() [(x﹣1)+
[(x﹣1)+ ![]() +2]≥2,
+2]≥2,
当且仅当x=2时取“=”成立,于是a≤2,
当a>2时,设h(x)=x2﹣2a(x﹣1),
∵h(2)=4﹣2a=2(2﹣a)>0,
又抛物线h(x)=x2﹣2a(x﹣1)开口向上,
故h(x)=x2﹣2a(x﹣1)有2个零点,
设两个零点为x1 , x2 , 则x1<2<x2 ,
于是x∈(2,x2)时,h(x)<0,故g′(x)<0,g(x)递减,
故g(x)<g(2)=0,与题设矛盾,不合题意,
综上,a的范围是(﹣∞,2].
【解析】(Ⅰ)求出函数的导数,计算f(2),f′(2),求出切线方程即可;(Ⅱ)设函数g(x)=ln(x﹣1)﹣ ![]() ,(x≥2),于是问题转化为g(x)≥0对任意的x≥2恒成立,根据函数的单调性求出a的范围即可.
,(x≥2),于是问题转化为g(x)≥0对任意的x≥2恒成立,根据函数的单调性求出a的范围即可.
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
