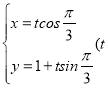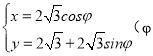题目内容
【题目】下列命题中不正确的个数是（ ）
①若直线
上有无数个点不在平面
内，则
；
②和两条异面直线都相交的两条直线异面；
③如果两条平行直线中的一条与一个平面平行，那么另一条也与这个平面平行；
④一条直线和两条异面直线都相交，则它们可以确定两个平面．
A.0B.1C.2D.3
【答案】D
【解析】
A：根据线面位置关系进行判断即可；
B：通过长方体举特例进行判断即可；
C：根据线面平行的性质进行判断即可；
D：根据确定平面定理，结合异面直线的定义进行判断即可.
A：当直线
与平面
相交时，直线上也存在有无数个点不在平面内，故本说法不正确；
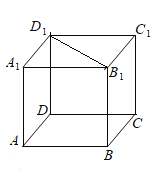
B：如下图，在长方体
中，
都与异面直线
都相交，而是相交直线，故本说法不正确；
C：如果两条平行直线中的一条与一个平面平行，那么另一条有可能在该平面内，故本说法不正确；
D：两个相交线可以确定一个平面，因此一条直线和两条异面直线都相交，一共能确定两个平面，如果这两个平面重合，这与异面直线的定义相矛盾，故本说法是正确的.
培优三好生系列答案
优化作业上海科技文献出版社系列答案
【题目】某学校为了了解初三学生的体育锻炼情况，随机抽取了40名学生对一周的体育锻炼时间长（单位：小时）进行统计，并将数据整理如下：
时间长 性别 |
|
|
|
|
|
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
（1）采用样本估计总体的方式，试估计该校的所有学生中一周的体育锻炼时间长为
的概率；
（2）若将一周的体育锻炼时间长不低于3小时的评定为“体育锻炼合格者”，否则为“不合格者”，根据以上数据完成下面的
列联表，并据此判断能否有95%的把握认为体育锻炼与性别有关？附：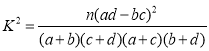
，其中
.
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【题目】全世界越来越关注环境保护问题，某监测站点于2016年8月某日起连续
天监测空气质量指数(
)，数据统计如下：
空气质量指数( | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 |
| 10 | 5 |
(1)根据所给统计表和频率分布直方图中的信息求出
的值，并完成频率分布直方图；
(2)在空气质量指数分别为51-100和151-200的监测数据中，用分层抽样的方法抽取5天，从中任意选取2天，求事件
“两天空气都为良”发生的概率.
