题目内容
【题目】已知函数![]() .
.
(1)若![]() ,且
,且![]() 在
在![]() 上单调递减,求
上单调递减,求![]() 的取值范围;
的取值范围;
(2)若![]() ,且
,且![]() 在区间
在区间![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() 时,求证:在区间
时,求证:在区间![]() 至少存在一个
至少存在一个![]() ,使得
,使得![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)根据二次函数![]() 在区间
在区间![]() 上单调递减得出
上单调递减得出![]() ,进而可求得实数
,进而可求得实数![]() 的取值范围;
的取值范围;
(2)由题意得出![]() 对任意的
对任意的![]() 恒成立,利用参变量分离法得出
恒成立,利用参变量分离法得出![]() ,求出函数
,求出函数![]() 在
在![]() 上的最大值,即可得出实数
上的最大值,即可得出实数![]() 的取值范围;
的取值范围;
(3)利用反证法,假设对任意的![]() ,均有
,均有![]() ,根据题意得出
,根据题意得出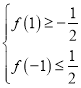 ,推出矛盾即可.
,推出矛盾即可.
(1)当![]() 时,
时,![]() ,该二次函数的图象开口向上,对称轴为直线
,该二次函数的图象开口向上,对称轴为直线![]() ,
,
由于函数![]() 在
在![]() 单调递减,则有
单调递减,则有![]() ,解得
,解得![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)由题可知![]() 在
在![]() 恒成立,则
恒成立,则![]() 且
且![]() ,
,
令![]() ,
,![]() ,则二次函数
,则二次函数![]() 在
在![]() 时单调递减,
时单调递减,
当![]() 时,函数
时,函数![]() 取得最大值,即
取得最大值,即![]() ,
,![]() ,
,
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(3)由题可知![]() ,且
,且![]() ,函数开口向上,对称轴
,函数开口向上,对称轴![]() ,
,
则![]() 在
在![]() 单调递减,其值域为
单调递减,其值域为![]() ,
,
若不存在![]() 使得
使得![]() ,即对任意
,即对任意![]() 都有
都有![]() ,
,
即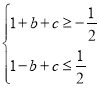 ,可得
,可得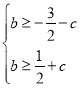 ,即
,即![]() ,与
,与![]() 矛盾.
矛盾.
故必存在![]() ,使得
,使得![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
【题目】甲、乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们射击成绩的分布列如下表所示.
射手甲 | 射手乙 | ||||||
环数 |
|
|
| 环数 |
|
|
|
概率 |
|
|
| 概率 |
|
|
|
(1)若甲射手共有![]() 发子弹,一旦命中
发子弹,一旦命中![]() 环就停止射击,求他剩余
环就停止射击,求他剩余![]() 发子弹的概率;
发子弹的概率;
(2)若甲、乙两名射手各射击![]() 次,求
次,求![]() 次射击中恰有
次射击中恰有![]() 次命中
次命中![]() 环的概率;
环的概率;
(3)若甲、乙两名射手各射击![]() 次,记所得的环数之和为
次,记所得的环数之和为![]() ,求
,求![]() 的概率分布.
的概率分布.