题目内容
【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选择意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果整理成条形图如下.
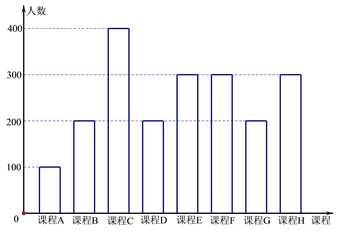
上图中,已知课程![]() 为人文类课程,课程
为人文类课程,课程![]() 为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取
为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取![]() 的学生作为研究样本组(以下简称“组M”).
的学生作为研究样本组(以下简称“组M”).
(Ⅰ)在“组M”中,选择人文类课程和自然科学类课程的人数各有多少?
(Ⅱ)为参加某地举办的自然科学营活动,从“组M”所有选择自然科学类课程的同学中随机抽取4名同学前往,其中选择课程F或课程H的同学参加本次活动,费用为每人1500元,选择课程G的同学参加,费用为每人2000元.
(ⅰ)设随机变量![]() 表示选出的4名同学中选择课程
表示选出的4名同学中选择课程![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列;
的分布列;
(ⅱ)设随机变量![]() 表示选出的4名同学参加科学营的费用总和,求随机变量
表示选出的4名同学参加科学营的费用总和,求随机变量![]() 的期望.
的期望.
【答案】(Ⅰ)12,8;(Ⅱ)(ⅰ) 见解析;(ⅱ)6500.
【解析】试题分析:(1)分层抽样即按比例抽样(2)根据题意在自然学科中抽4人即![]() ,然后设随机变量
,然后设随机变量![]() 表示选出的4名同学中选择课程
表示选出的4名同学中选择课程![]() 的人数故随机变量
的人数故随机变量![]() 可取0,1,2.再根据超几何分布一一列式即可写出分布列再求期望(3)设随机变量
可取0,1,2.再根据超几何分布一一列式即可写出分布列再求期望(3)设随机变量![]() 表示选出的4名同学参加科学营的费用总和,则随机变量
表示选出的4名同学参加科学营的费用总和,则随机变量![]() =6000+500
=6000+500![]() 所以E(
所以E(![]() )=6000+500E(
)=6000+500E(![]() )
)
试题解析:
(Ⅰ)选择人文类课程的人数为(100+200+400+200+300) ![]() 1%=12(人);
1%=12(人);
选择自然科学类课程的人数为(300+200+300) ![]() 1%=8(人).
1%=8(人).
(Ⅱ)(ⅰ)依题意,随机变量![]() 可取0,1,2.
可取0,1,2.
![]() ;
; ![]() ;
; ![]()
故随机变量![]() 的分布列为
的分布列为
X | 0 | 1 | 2 |
p |
|
|
|
(ⅱ)法1:依题意,随机变量![]() =2000
=2000![]() +1500
+1500![]() =6000+500
=6000+500![]() ,
,
所以随机变量![]() 的数学期望为
的数学期望为
E(![]() )=6000+500E(
)=6000+500E(![]() )=6000+500(
)=6000+500(![]() )=6500.
)=6500.
(ⅱ)法2:依题意,随机变量![]() 可取6000,6500,7000.
可取6000,6500,7000.
所以随机变量![]() 的分布列为
的分布列为
Y | 6000 | 6500 | 7000 |
p |
|
|
|
所以随机变量![]() 的数学期望为E(
的数学期望为E(![]() )=
)=![]() =6500.
=6500.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案【题目】几个月前,成都街头开始兴起“mobike”、“ofo”等共享单车,这样的共享单车为很多市民解决了最后一公里的出行难题.然而,这种模式也遇到了一些让人尴尬的问题,比如乱停乱放,或将共享单车占为“私有”等.
为此,某机构就是否支持发展共享单车随机调查了50人,他们年龄的分布及支持发展共享单车的人数统计如下表:
年龄 |
|
|
|
|
|
|
受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
支持发展 共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系;
列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系;
年龄低于35岁 | 年龄不低于35岁 | 合计 | |
支持 | |||
不支持 | |||
合计 |
(Ⅱ)若对年龄在![]() ,
,![]() 的被调查人中各随机选取两人进行调查,记选中的4人中支持发展共享单车的人数为
的被调查人中各随机选取两人进行调查,记选中的4人中支持发展共享单车的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.