题目内容
17.已知数列{an}的前n项和Sn满足an+1=2Sn+6,且a1=6.(1)求a2的值;
(2)求数列{an}的通项公式;
(3)设${b_n}=\frac{{2{a_n}}}{{({3^n}-1)({S_n}+2)}}$,证明:b1+b2+…+bn<1.
分析 (1)令n=1,由a1=S1,即可得到所求;
(2)将n换成n-1,两式相减,再结合等比数列的定义和通项公式,计算即可得到所求;
(3)求出Sn,可得bn,再由裂项相消求和,计算即可得证.
解答 解:(1)当n=1时,a2=2S1+6=2a1+6=18,∴a2=18;
(2)由an+1=2Sn+6①,得an=2Sn-1+6(n≥2)②
①-②:得an+1-an=2Sn-2Sn-1,
即an+1=3an(n≥2),
又a1=6,a2=18,所以a2=3a1,
∴数列{an}是以6为首项,公比为3的等比数列,
∴${a_n}=6•{3^{n-1}}=2•{3^n}$;
(3)证明:由(2)得:${a_{n+1}}=2•{3^{n+1}}$,
故${S_n}=\frac{1}{2}{a_{n+1}}-3={3^{n+1}}-3$,${b_n}=\frac{{2{a_n}}}{{({3^n}-1)({S_n}+2)}}=\frac{{4•{3^n}}}{{({3^n}-1)({3^{n+1}}-1)}}=\frac{{2({3^{n+1}}-1)-({3^n}-1)}}{{({3^n}-1)({3^{n+1}}-1)}}=2({\frac{1}{{{3^n}-1}}-\frac{1}{{{3^{n+1}}-1}}})$
∴${b_1}+{b_2}+…+{b_n}=2(\frac{1}{{{3^1}-1}}-\frac{1}{{{3^2}-1}}+\frac{1}{{{3^2}-1}}-\frac{1}{{{3^3}-1}}+…+\frac{1}{{{3^n}-1}}-\frac{1}{{{3^{n+1}}-1}})$
=$2•(\frac{1}{2}-\frac{1}{{{3^{n+1}}-1}})<1$.
点评 本题考查数列的通项和求和,主要考查等比数列的通项和数列的求和方法:裂项求和,考查运算能力,属于中档题.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案| A. | {1} | B. | {2} | C. | {0,1} | D. | {1,2} |
| A. | 12 | B. | 13 | C. | 11 | D. | 14 |
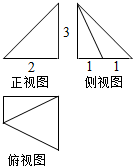
| A. | $\sqrt{14}$ | B. | $\sqrt{13}$ | C. | $\sqrt{5}$ | D. | 4 |