题目内容
9．某几何体的三视图如图所示，且该几何体的所有棱中，则该几何体的所有棱中，最长的棱为（ ）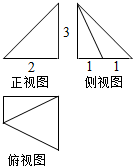
| A． | $\sqrt{14}$ | B． | $\sqrt{13}$ | C． | $\sqrt{5}$ | D． | 4 |
分析 根据三视图判断几何体为四棱锥，再利用体积公式求高x即可．
解答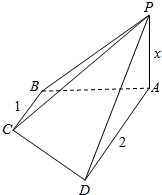 
解：根据三视图判断几何体为四棱锥，其直观图如图：AB=AD=2，BC=1，AB⊥BC，AB⊥AD，AC=$\sqrt{5}$，
V=$\frac{1}{3}$×$\frac{1+2}{2}$×2×x=3⇒x=3．
PA=x=3，AC＞AD=AB，∴PC最长，PC=$\sqrt{{3}^{2}+（\sqrt{5}）^{2}}$=$\sqrt{14}$．
故选：A．
点评 本题考查由三视图求几何体的体积．几何体的点、线、面距离的求法，考查计算能力．
练习册系列答案
期末集结号系列答案
相关题目
一个盒子中装有大量形状大小一样但重量不尽相同的小球，从中随机抽取50个作为样本，称出它们的重量（单位：克），重量分组区间为[5，15]，（15，25]，（25，35]，（35，45]，由此得到样本的重量频率分布直方图（如图）．
已知椭圆$E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右焦点分别为F1，F2及椭圆的短轴端点为顶点的三角形是等边三角形，椭圆的右顶点到右焦点的距离为1
14．在等腰△ABC中，∠BAC=90°，AB=AC=2，$\overrightarrow{BC}=2\overrightarrow{BD}$，$\overrightarrow{AC}=3\overrightarrow{AE}$，则$\overrightarrow{AD}•\overrightarrow{BE}$的值为（ ）
| A． | $-\frac{4}{3}$ | B． | $-\frac{1}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{4}{3}$ |
如图，某几何体的三视图均为边长为2的正方形，则该几何体的体积是$\frac{20}{3}$．
18．如图所示的程序框图的输出结果是（ ）
| A． | 2 | B． | $\frac{1}{2}$ | C． | -$\frac{1}{2}$ | D． | -1 |
19．函数f（x）=x2-4x-2lnx+5的零点个数为（ ）
| A． | 3 | B． | 2 | C． | 1 | D． | 0 |