题目内容
5.已知△ABC中,设三个内角A,B,C所对的边长分别为a,b,c,且$a=1,b=\sqrt{3},A=\frac{π}{6}$,则c=1或2.分析 由已知结合正弦定理可求sinB,B为三角形内角,由三角形内角和定理从而可求B,C,利用正弦定理即可求c的值.
解答 解:由正弦定理可得:sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{3}×\frac{1}{2}}{1}$=$\frac{\sqrt{3}}{2}$,
所以B=$\frac{π}{3}$或$\frac{2π}{3}$,
故C=π-A-B=$\frac{π}{2}$或$\frac{π}{6}$,
由正弦定理可得:c=$\frac{asinC}{sinA}$=$\frac{1}{\frac{1}{2}}$=2,或c=$\frac{asinC}{sinA}$=$\frac{1×\frac{1}{2}}{\frac{1}{2}}$=1.
故答案为:1或2.
点评 本题主要考查了三角形内角和定理,正弦定理的应用,属于基本知识的考查.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
10.为了了解潮州市居民月用电情况,抽查了该市100户居民月用电量(单位:度),得到频率分布直方图如下:根据下图可得这100户居民月用电量在〔150,300〕的用户数是( )

| A. | 70 | B. | 64 | C. | 48 | D. | 30 |
14.一个四棱锥的三视图如图所示,那么这个四棱锥的表面积是( )
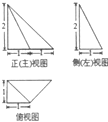

| A. | $\frac{{9+2\sqrt{3}+\sqrt{5}}}{2}$ | B. | $\frac{{9+2\sqrt{3}}}{2}$ | C. | $\frac{{9+2\sqrt{5}}}{2}$ | D. | $\frac{{11+\sqrt{5}}}{2}$ |

 已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2及椭圆的短轴端点为顶点的三角形是等边三角形,椭圆的右顶点到右焦点的距离为1
已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2及椭圆的短轴端点为顶点的三角形是等边三角形,椭圆的右顶点到右焦点的距离为1