题目内容
16.正四面体ABCD的表面积为S,其中四个面的中心分别是E、F、G、H.设四面体EFGH的表面积为T,则$\frac{T}{S}$等于$\frac{1}{9}$.分析 因为正四面体四个面都是正△,其中心到顶点的距离等于到对边距离的一半,通过作出辅助线,可得两四面体的边长比,由面积比是边长比的平方,可得出答案
解答 解:解:如图所示,正四面体ABCD四个面的中心分别为E、F、G、H,
∴四面体EFGH也是正四面体.
连接AE并延长与CD交于点M,
连接AG并延长与BC交于点N.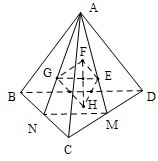
∵E、G分别为面的中心,
∴$\frac{AE}{AM}$=$\frac{AG}{AN}$=$\frac{2}{3}$.
∴$\frac{GE}{MN}$=$\frac{2}{3}$.
又∵MN=$\frac{1}{2}$BD,
∴$\frac{GE}{BD}$=$\frac{1}{3}$.
∵面积比是相似比的平方,
∴两四面体的面积比为$\frac{T}{S}$=$\frac{1}{9}$.
故答案为:$\frac{1}{9}$
点评 本题考查了多面体的面积比是边长比的平方,本题关键是求边长比是多少;类似的有体积比是边长比的立方,三角形的高,中线,角平分线的比等于边长的比

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
7.设z=1-i(i为虚数单位),则z2+$\frac{2}{z}$的共轭复数是( )
| A. | -1-i | B. | -1+i | C. | 1-i | D. | 1+i |
1.若G是△ABC的重心,且$a\overrightarrow{G{A}}+b\overrightarrow{G{B}}+\frac{{\sqrt{3}}}{3}c\overrightarrow{GC}=\vec 0$,则角A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
5.当-1<m<1时,复数z=$\frac{-1+i}{m+i}$(i为虚数单位)在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图所示,AB是半径为1的圆的直径,过点A,B分别引弦AD和BE,相交于点C,过点C作CF⊥AB,垂足为点F.已知∠CAB=30°,∠DCB=60°.
如图所示,AB是半径为1的圆的直径,过点A,B分别引弦AD和BE,相交于点C,过点C作CF⊥AB,垂足为点F.已知∠CAB=30°,∠DCB=60°.