题目内容
【题目】如图,在多面体ABCDNPM中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,AB=AP=2,PM∥AB,PN∥AD,PM=PN=1.
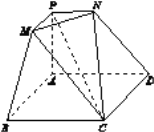
(1)求证:MN⊥PC;
(2)求平面MNC与平面APMB所成锐二面角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)先利用平行关系证明线线平行,利用菱形的对角线垂直、线面垂直的判定和性质进行证明;(2)建立适当的空间直角坐标系,写出相关点的坐标,求出有关直线的方向向量和平面的法向量,再利用空间向量的夹角公式进行求解.
试题解析:(1)证明:作ME∥PA交AB于E,NF∥PA交AD于F,连接EF,BD,AC.
由PM∥AB,PN∥AD,易得![]() ,所以四边形MEFN是平行四边形,
,所以四边形MEFN是平行四边形,
所以MN∥EF,因为底面ABCD是菱形,所以AC⊥BD,又易得EF∥BD,所以AC⊥EF,所以AC⊥MN,
因为PA⊥平面ABCD,EF![]() 平面ABCD,所以PA⊥EF,所以PA⊥MN,因为AC∩PA=A,
平面ABCD,所以PA⊥EF,所以PA⊥MN,因为AC∩PA=A,
所以MN⊥平面PAC,故MN⊥PC.
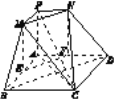
(2)建立空间直角坐标系如图所示,
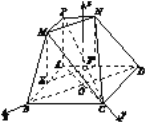
则C(0,1,0),M![]() ,N
,N![]() ,A(0,-1,0),P(0,-1,2),B(
,A(0,-1,0),P(0,-1,2),B(![]() ,0,0),
,0,0),
所以![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =(0,0,2),
=(0,0,2),![]() =(
=(![]() ,1,0),设平面MNC的法向量为m=(x,y,z),则
,1,0),设平面MNC的法向量为m=(x,y,z),则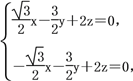 令z=1,得x=0,y=
令z=1,得x=0,y=![]() ,所以m=
,所以m=![]() ;
;
设平面APMB的法向量为n=(x1,y1,z1),则![]()
令x1=1,得y1=-![]() ,z1=0,所以n=(1,-
,z1=0,所以n=(1,-![]() ,0),
,0),
设平面MNC与平面APMB所成锐二面角为α,
则cos α=![]() =
=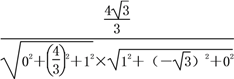 =
=![]() ,
,
所以平面MNC与平面APMB所成锐二面角的余弦值为![]() .
.

【题目】已知某运动员每次投篮命中的概率为80%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4,5,6,7,8表示命中,9,0表示未命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 | 966 | 191 | 925 | 271 | 932 | 812 | 458 | 569 | 683 |
431 | 257 | 393 | 027 | 556 | 488 | 730 | 113 | 537 | 989 |
据此估计,该运动员三次投篮均命中的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()