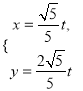题目内容
【题目】在直角坐标系中,以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且点
,且点![]() 在直线
在直线![]() 上.
上.
(1)求![]() 的值及直线
的值及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)圆![]() 的极坐标方程为
的极坐标方程为![]() ,试判断直线
,试判断直线![]() 与圆
与圆![]() 的位置关系.
的位置关系.
【答案】(1)![]() ; (2)见解析.
; (2)见解析.
【解析】
(1)由点A在直线l上,代入可得![]() cos(
cos(![]() )=a,解得a.由ρcos(θ
)=a,解得a.由ρcos(θ![]() )
)![]() ,展开化为:
,展开化为:![]() ,利用互化公式即可得出.
,利用互化公式即可得出.
(2)圆C的极坐标方程为ρ=2cosα,即ρ2=2ρcosα,化为:(x﹣1)2+y2=1.可得圆心,半径,求出圆心到直线的距离d,与半径r比较大小关系,即可得出.
(1)由点![]() 在直线
在直线![]() 上,可得
上,可得![]() ,
,
所以直线![]() 的方程可化为
的方程可化为![]() ,
,
从而直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)由已知得圆![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
所以圆心为![]() ,半径
,半径![]() ,所以圆心到直线的距离
,所以圆心到直线的距离![]() ,
,
所以直线![]() 与圆
与圆![]() 相交.
相交.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
【题目】某市化工厂三个车间共有工人1000名,各车间男、女工人数如下表:已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0.15.
第一车间 | 第二车间 | 第三车间 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
(1)求x的值.
(2)现用分层抽样的方法在全厂抽取50名工人,则应在第三车间抽取多少名工人?