题目内容
(本题满分15分)
已知a、b∈(0,+∞),且a+b=1,
求证:(1) ab≤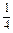 (2)
(2)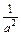 +
+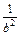 ≥8; (3)
≥8; (3) 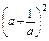 +
+ 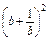 ≥
≥ . (5分+5分+5分)
. (5分+5分+5分)
已知a、b∈(0,+∞),且a+b=1,
求证:(1) ab≤
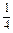 (2)
(2)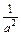 +
+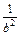 ≥8; (3)
≥8; (3) 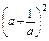 +
+ 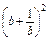 ≥
≥ . (5分+5分+5分)
. (5分+5分+5分)证明 (1) 由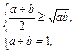 a、b∈(0,+∞),
a、b∈(0,+∞),
得 ≤
≤
 ab≤
ab≤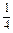

 ≥4.
≥4.
(当且仅当a=b= 时取等号)
时取等号)
(2)∵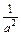 +
+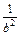 ≥
≥ ≥8,∴
≥8,∴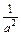 +
+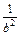 ≥8.
≥8.
(3)∵a2+b2=(a+b)2-2ab=1-2ab≥1-2×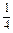 =
= ,∴a2+b2≥
,∴a2+b2≥ .
.
∴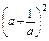 +
+ 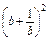 =a2+b2+4+
=a2+b2+4+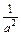 +
+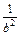
≥ +4+8=
+4+8= ,∴
,∴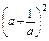 +
+ 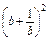 ≥
≥ .------------------------------13分
.------------------------------13分
(当且仅当a=b= 时取等号) ---------------------------------15分
时取等号) ---------------------------------15分
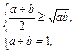 a、b∈(0,+∞),
a、b∈(0,+∞),得
 ≤
≤
 ab≤
ab≤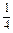

 ≥4.
≥4.(当且仅当a=b=
 时取等号)
时取等号)(2)∵
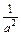 +
+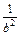 ≥
≥ ≥8,∴
≥8,∴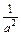 +
+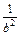 ≥8.
≥8.(3)∵a2+b2=(a+b)2-2ab=1-2ab≥1-2×
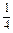 =
= ,∴a2+b2≥
,∴a2+b2≥ .
.∴
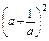 +
+ 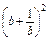 =a2+b2+4+
=a2+b2+4+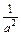 +
+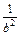
≥
 +4+8=
+4+8= ,∴
,∴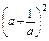 +
+ 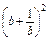 ≥
≥ .------------------------------13分
.------------------------------13分(当且仅当a=b=
 时取等号) ---------------------------------15分
时取等号) ---------------------------------15分略

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 ,则
,则 的最小值为
的最小值为

 ( )
( )

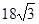
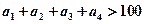 ,
, 中,至少有一个数大于25
中,至少有一个数大于25 
 是不相等的正数.用分析法证明
是不相等的正数.用分析法证明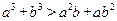 .
.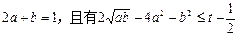 恒成立,则实数t的取值范围是 .
恒成立,则实数t的取值范围是 . 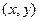 满足约束条件
满足约束条件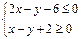 ,若目标函数
,若目标函数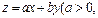
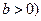 的最大值为40,则
的最大值为40,则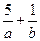 的最小值为: .
的最小值为: .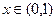 则
则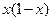 的最大值为 ▲
的最大值为 ▲ 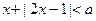 的解集为
的解集为 ,则实数a的取值集合是______________.
,则实数a的取值集合是______________. 的最大值是
的最大值是