题目内容
(本题满分16分)
已知数列{an}满足Sn+an=2n+1,
(1) 写出a1, a2, a3,并推测an的表达式;
(2) 用数学归纳法证明所得的结论。
已知数列{an}满足Sn+an=2n+1,
(1) 写出a1, a2, a3,并推测an的表达式;
(2) 用数学归纳法证明所得的结论。
(1) a1=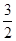 , a2=
, a2=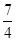 , a3=
, a3=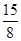 , 猜测 an=2-
, 猜测 an=2-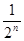 (2)见解析
(2)见解析
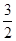 , a2=
, a2=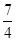 , a3=
, a3=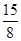 , 猜测 an=2-
, 猜测 an=2-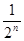 (2)见解析
(2)见解析解: (1) a1=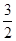 , a2=
, a2=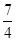 , a3=
, a3=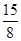 , 猜测 an=2-
, 猜测 an=2-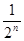 ……5分
……5分
(2) ①由(1)已得当n=1时,命题成立;……8分
②假设n=k时,命题成立,即 ak=2-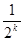 , ……10分
, ……10分
当n=k+1时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,且a1+a2+……+ak=2k+1-ak
∴2k+1-ak+2ak+1=2(k+1)+1=2k+3,
∴2ak+1=2+2-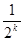 , ak+1=2-
, ak+1=2-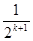 , 即当n=k+1时,命题成立. ……15分
, 即当n=k+1时,命题成立. ……15分
根据①②得n∈N+ , an=2-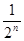 都成立 ……16分
都成立 ……16分
思路分析:第一问利用Sn+an=2n+1,递推得到a1=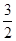 , a2=
, a2=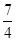 , a3=
, a3=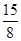 , 猜测 an=2-
, 猜测 an=2-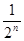
第二问中,1)已得当n=1时,命题成立;
②假设n=k时,命题成立,即 ak=2-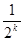 ,当n=k+1时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,且a1+a2+……+ak=2k+1-ak
,当n=k+1时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,且a1+a2+……+ak=2k+1-ak
∴2k+1-ak+2ak+1=2(k+1)+1=2k+3,
∴2ak+1=2+2-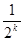 , ak+1=2-
, ak+1=2-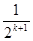
综上可知成立。
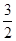 , a2=
, a2=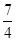 , a3=
, a3=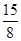 , 猜测 an=2-
, 猜测 an=2-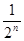 ……5分
……5分(2) ①由(1)已得当n=1时,命题成立;……8分
②假设n=k时,命题成立,即 ak=2-
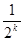 , ……10分
, ……10分当n=k+1时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,且a1+a2+……+ak=2k+1-ak
∴2k+1-ak+2ak+1=2(k+1)+1=2k+3,
∴2ak+1=2+2-
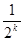 , ak+1=2-
, ak+1=2-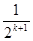 , 即当n=k+1时,命题成立. ……15分
, 即当n=k+1时,命题成立. ……15分 根据①②得n∈N+ , an=2-
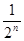 都成立 ……16分
都成立 ……16分思路分析:第一问利用Sn+an=2n+1,递推得到a1=
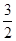 , a2=
, a2=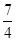 , a3=
, a3=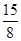 , 猜测 an=2-
, 猜测 an=2-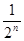
第二问中,1)已得当n=1时,命题成立;
②假设n=k时,命题成立,即 ak=2-
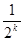 ,当n=k+1时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,且a1+a2+……+ak=2k+1-ak
,当n=k+1时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,且a1+a2+……+ak=2k+1-ak∴2k+1-ak+2ak+1=2(k+1)+1=2k+3,
∴2ak+1=2+2-
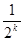 , ak+1=2-
, ak+1=2-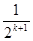
综上可知成立。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
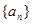 的前n项和
的前n项和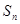 满足:
满足: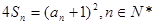 ,
,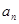 和前n项和
和前n项和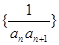 的前n项和
的前n项和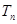 ;
;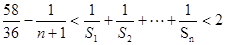 对任意的
对任意的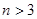 ,
,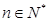 都成立.
都成立.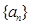 前
前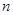 项和为
项和为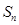 , 满足
, 满足 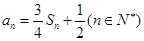 .
.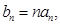 求数列
求数列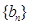 的前
的前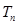 ;
;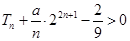 对任意的
对任意的 恒成立,求实数
恒成立,求实数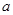 的取值范围.
的取值范围.
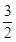 ,bn+1=-
,bn+1=-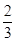 Sn(n∈N*).
Sn(n∈N*).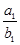 +
+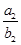 +…+
+…+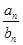 ,求Tn的表达式
,求Tn的表达式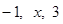 ,则它的第五项为 .
,则它的第五项为 .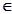 N*,均有S n>0
N*,均有S n>0 }的前4项的和为20,且
}的前4项的和为20,且 成等比数列;
成等比数列; ,求数列{
,求数列{ }的前n项的和
}的前n项的和 ;
;
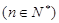 使得
使得 成立?若存在,求出所有解;若不存在,请说明理由.
成立?若存在,求出所有解;若不存在,请说明理由. 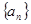 的前
的前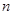 项和为
项和为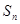 ,
,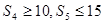 ,则
,则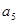 的最大值是 .
的最大值是 .