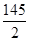题目内容
设数列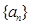 前
前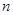 项和为
项和为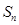 , 满足
, 满足 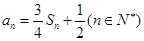 .
.
(1)求数列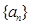 的通项公式;
的通项公式;
(2)令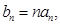 求数列
求数列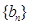 的前
的前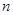 项和
项和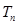 ;
;
(3)若不等式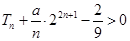 对任意的
对任意的 恒成立,求实数
恒成立,求实数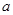 的取值范围.
的取值范围.
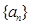 前
前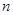 项和为
项和为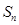 , 满足
, 满足 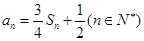 .
.(1)求数列
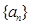 的通项公式;
的通项公式;(2)令
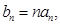 求数列
求数列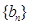 的前
的前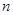 项和
项和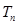 ;
;(3)若不等式
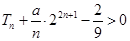 对任意的
对任意的 恒成立,求实数
恒成立,求实数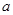 的取值范围.
的取值范围.(1)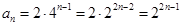 .
.
(2)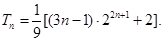
(3)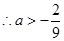
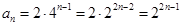 .
. (2)
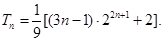
(3)
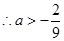
根据递推公式,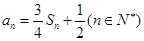 ,用到
,用到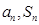 的关系,
的关系,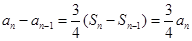 ,
,
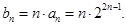 是差比数列,其和用错位相减法,注意相同次数的对齐,得
是差比数列,其和用错位相减法,注意相同次数的对齐,得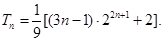
恒成立问题通常将参数分离出来,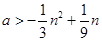 在最值处成立即可
在最值处成立即可
解(1)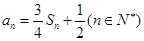
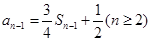
两式相减,得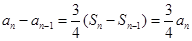 . 所以,
. 所以,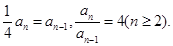
又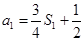 ,即
,即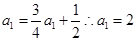
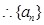 是首项为
是首项为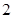 ,公比是
,公比是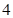 的等比数列.所以
的等比数列.所以 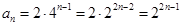 .
.
(2)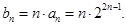
 ①
①
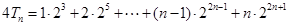 ②
②
①-②,得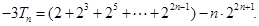
故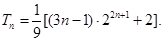 ……………7分
……………7分
(3)由题意,再结合(2),知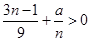
即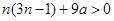 .
.
从而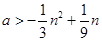
设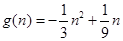 ,
,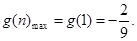
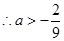
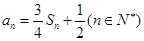 ,用到
,用到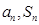 的关系,
的关系,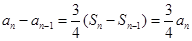 ,
,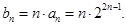 是差比数列,其和用错位相减法,注意相同次数的对齐,得
是差比数列,其和用错位相减法,注意相同次数的对齐,得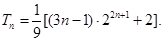
恒成立问题通常将参数分离出来,
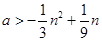 在最值处成立即可
在最值处成立即可解(1)
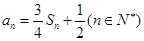
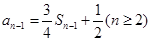
两式相减,得
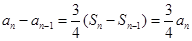 . 所以,
. 所以,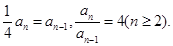
又
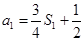 ,即
,即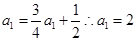
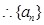 是首项为
是首项为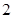 ,公比是
,公比是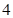 的等比数列.所以
的等比数列.所以 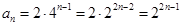 .
. (2)
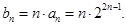
 ①
①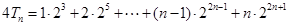 ②
②①-②,得
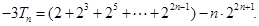
故
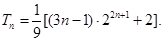 ……………7分
……………7分(3)由题意,再结合(2),知
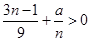
即
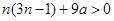 .
.从而
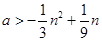
设
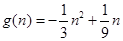 ,
,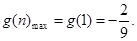

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
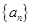 满足
满足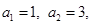
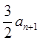 是
是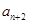 与
与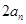 的等差中项
的等差中项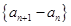 是等比数列;
是等比数列;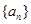 中,
中,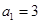 ,前
,前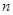 项和为
项和为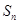 ,等比数列
,等比数列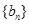 各项均为正数,
各项均为正数,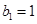 ,且
,且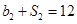 ,
,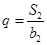
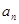 与
与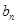 ;
;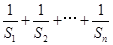
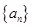 是等差数列,
是等差数列,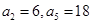 ;数列
;数列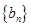 的前n项和是
的前n项和是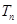 ,且
,且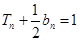 .
.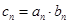 ,求
,求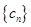 的前n项和
的前n项和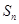
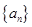 中,
中, ,
,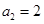 ,
,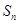 是数列
是数列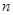 项和,且
项和,且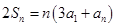 ,
,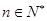 .
. 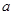 的值;
的值;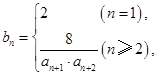
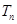 是数列
是数列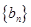 的前
的前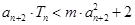 对一切
对一切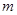 取值范围.
取值范围.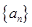 满足
满足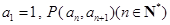 在直线
在直线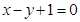 上,如果函数
上,如果函数
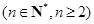 ,则函数
,则函数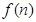 的最小值为
的最小值为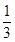


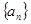 为等差数列,公差为
为等差数列,公差为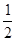 ,且
,且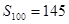 ,则
,则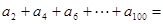 ( )
( )