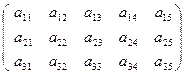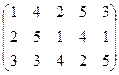题目内容
已知正项数列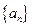 满足:
满足: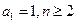 时,
时,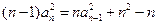 。
。
(1)求数列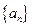 的通项公式;
的通项公式;
(2)设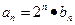 ,数列
,数列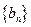 的前n项和为
的前n项和为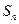 ,是否存在正整数m,使得对任意的
,是否存在正整数m,使得对任意的
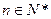 ,
,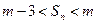 恒成立?若存在,求出所有的正整数m;若不存在,说明理由。
恒成立?若存在,求出所有的正整数m;若不存在,说明理由。
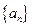 满足:
满足: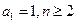 时,
时,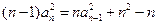 。
。(1)求数列
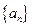 的通项公式;
的通项公式;(2)设
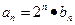 ,数列
,数列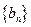 的前n项和为
的前n项和为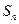 ,是否存在正整数m,使得对任意的
,是否存在正整数m,使得对任意的
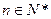 ,
,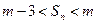 恒成立?若存在,求出所有的正整数m;若不存在,说明理由。
恒成立?若存在,求出所有的正整数m;若不存在,说明理由。解:①由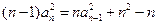
得
令 ∴
∴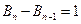 (
(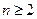 )
)
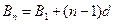 而
而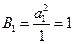
∴ 即
即
即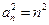 ,由正项数列知
,由正项数列知 ………………6分
………………6分
②由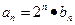 得
得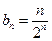

∴ 的
的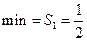 而
而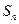 的
的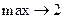
∴当m=2或m=3时
使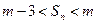 恒成立……
恒成立…… …………13分
…………13分
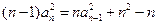
得

令
 ∴
∴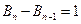 (
(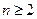 )
)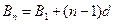 而
而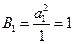
∴
 即
即
即
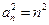 ,由正项数列知
,由正项数列知 ………………6分
………………6分②由
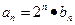 得
得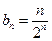

∴
 的
的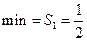 而
而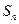 的
的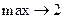
∴当m=2或m=3时
使
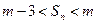 恒成立……
恒成立…… …………13分
…………13分略

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
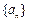 的前n项和
的前n项和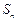 满足:
满足: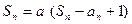 (
(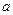 为常数,
为常数,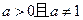 ).
).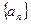 的通项公式;
的通项公式;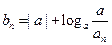 ,若数列
,若数列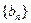 的前n项和
的前n项和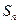 中,
中,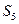 为最大值,求
为最大值,求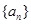 的前
的前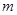 项和为30,前
项和为30,前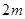 项和为100,则它的前
项和为100,则它的前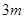 项和是( )
项和是( ) }的前
}的前 项和为
项和为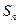 ,已知5
,已知5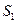 、2
、2 、
、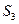 成等差数列.
成等差数列. ;
; -
-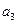 =3且
=3且 时,求
时,求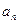 }和{
}和{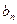 }满足:对于任何
}满足:对于任何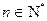 ,有
,有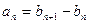 ,
,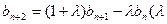 为非零常数),且
为非零常数),且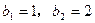 .
.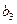 是
是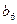 与
与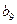 的等差中项,试求
的等差中项,试求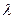 的值,并研究:对任意的
的值,并研究:对任意的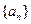 的前n项和为
的前n项和为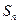 ,
,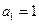 ,
, ,等差数列
,等差数列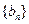 中,
中,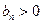
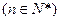 ,且
,且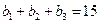 ,又
,又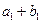 、
、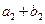 、
、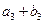 成等比数列.
成等比数列.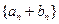 的前n项和Tn.
的前n项和Tn.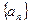 的公差
的公差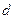 大于0,且
大于0,且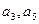 是方程
是方程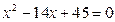 的两根,数列
的两根,数列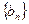 的前
的前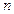 项的和为
项的和为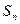 ,且
,且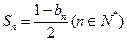 .
.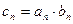 ,求证:
,求证: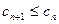 ;
;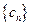 的前
的前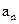 ﹜中,
﹜中, =
=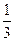 ,前n项和
,前n项和 满足
满足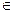 N*
N* )
)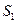 ,t(
,t(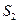 ), 3(
), 3(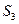 )成等差数列,求实数t的值。
)成等差数列,求实数t的值。 表示第
表示第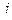 行第
行第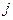 列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列
列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列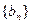 。规则如下:(1)先取出
。规则如下:(1)先取出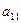 ,并记
,并记 ;若
;若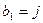 ,则从第
,则从第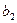 ;(2)以此类推,当
;(2)以此类推,当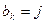 时,就从第
时,就从第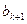 ;直到无法进行就终止。例如由(表(2)可以得到数列
;直到无法进行就终止。例如由(表(2)可以得到数列 ,5,3,2,5,1,3,1. 试问数列
,5,3,2,5,1,3,1. 试问数列