题目内容
(本小题满分12分)
已知数列
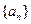 的前n项和为
的前n项和为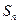 ,
,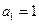 ,
, ,等差数列
,等差数列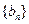 中,
中,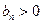
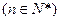 ,且
,且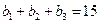 ,又
,又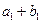 、
、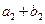 、
、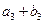 成等比数列.
成等比数列.(Ⅰ)求数列
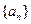 、
、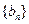 的通项公式;
的通项公式;(Ⅱ)求数列
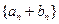 的前n项和Tn.
的前n项和Tn.(1)
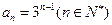 ∴bn=2n+1
∴bn=2n+1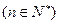 ,
, (2)
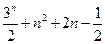
解:(Ⅰ)∵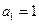 ,
, ,
,
∴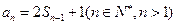 ,
,
∴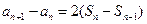 ,
, 
∴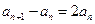 ,
,
∴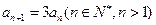 ………………………2分
………………………2分
而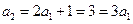 ,∴
,∴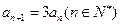
∴数列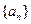 是以1为首项,3为公比的等比数列,
是以1为首项,3为公比的等比数列,
∴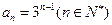 ………………………4分
………………………4分
∴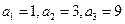 ,
,
在等差数列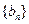 中,∵
中,∵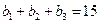 ,∴
,∴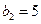 。
。
又因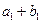 、
、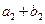 、
、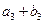 成等比数列,设等差数列
成等比数列,设等差数列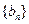 的公差为d,
的公差为d,
∴(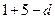 )
)
 ………
……… ………………………7分
………………………7分
解得d=-10,或d="2," ∵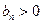
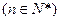 ,∴舍去d=-10,取d=2, ∴b1="3,"
,∴舍去d=-10,取d=2, ∴b1="3," 
∴bn=2n+1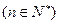 , ……………………………8分
, ……………………………8分
(Ⅱ)由(Ⅰ)知
∴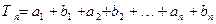
=(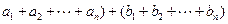
=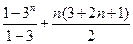
=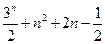 ………………………………12分
………………………………12分
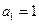 ,
, ,
,∴
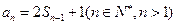 ,
,∴
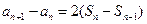 ,
, 
∴
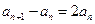 ,
, ∴
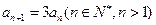 ………………………2分
………………………2分而
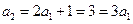 ,∴
,∴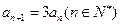
∴数列
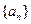 是以1为首项,3为公比的等比数列,
是以1为首项,3为公比的等比数列,∴
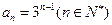 ………………………4分
………………………4分∴
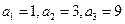 ,
, 在等差数列
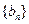 中,∵
中,∵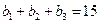 ,∴
,∴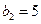 。
。又因
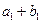 、
、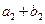 、
、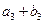 成等比数列,设等差数列
成等比数列,设等差数列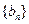 的公差为d,
的公差为d,∴(
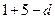 )
)
 ………
……… ………………………7分
………………………7分解得d=-10,或d="2," ∵
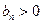
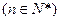 ,∴舍去d=-10,取d=2, ∴b1="3,"
,∴舍去d=-10,取d=2, ∴b1="3," 
∴bn=2n+1
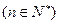 , ……………………………8分
, ……………………………8分(Ⅱ)由(Ⅰ)知
∴
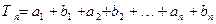
=(
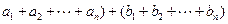
=
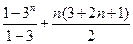
=
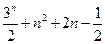 ………………………………12分
………………………………12分
练习册系列答案
相关题目
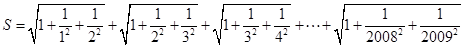 ,则不大于S的最大整数[S]等于()
,则不大于S的最大整数[S]等于() 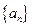 满足:
满足: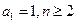 时,
时,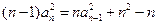 。
。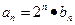 ,数列
,数列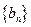 的前n项和为
的前n项和为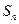 ,是否存在正整数m,使得对任意的
,是否存在正整数m,使得对任意的
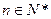 ,
,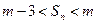 恒成立?若存在,求出所有的正整数m;若不存在,说明理由。
恒成立?若存在,求出所有的正整数m;若不存在,说明理由。 满足
满足 ,
, ,则
,则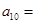 ( )
( ) 的前
的前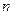 项和为
项和为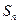 ,对
,对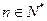 ,都有
,都有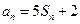 成立,
成立, ,试求数列
,试求数列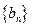 的前
的前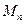 .
.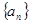 中,首项
中,首项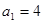 .公差
.公差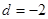 .则通过公式
.则通过公式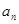 等于( )
等于( )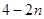
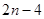
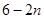
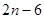
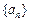 中,
中,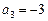 ,
,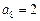 ,则
,则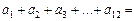
 7
7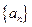 满足
满足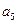 = 11,
= 11, 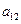 = -3,
= -3,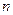 项和
项和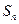 的最大值为
的最大值为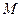 ,则
,则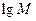 =
= 
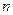 行有
行有
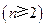 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如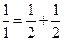 ,
, ,
,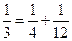 ,…,则第7行第4个数(从左往右数)为( )
,…,则第7行第4个数(从左往右数)为( )