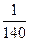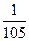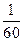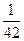题目内容
等差数列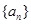 的前
的前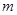 项和为30,前
项和为30,前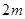 项和为100,则它的前
项和为100,则它的前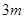 项和是( )
项和是( )
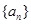 的前
的前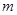 项和为30,前
项和为30,前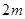 项和为100,则它的前
项和为100,则它的前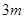 项和是( )
项和是( )| A.130 | B.170 | C.210 | D.260 |
C
分析:利用等差数列的前n项和公式,结合已知条件列出关于a1,d的方程组,用m表示出a1、d,进而求出s3m;或利用等差数列的性质,sm,s2m-sm,s3m-s2m成等差数列进行求解.
解答:解:解法1:设等差数列{an}的首项为a1,公差为d,
由题意得方程组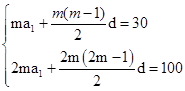 ,
,
解得d=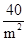 ,a1=
,a1=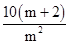 ,
,
∴s3m=3ma1+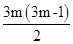
d=3m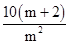 +
+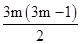 ×
×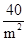 =210.
=210.
故选C.
解法2:∵设{an}为等差数列,
∴sm,s2m-sm,s3m-s2m成等差数列,
即30,70,s3m-100成等差数列,
∴30+s3m-100=70×2,
解得s3m=210.
故选C.
解答:解:解法1:设等差数列{an}的首项为a1,公差为d,
由题意得方程组
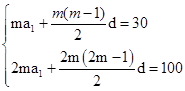 ,
,解得d=
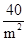 ,a1=
,a1=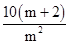 ,
,∴s3m=3ma1+
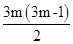
d=3m
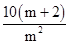 +
+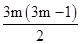 ×
×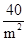 =210.
=210.故选C.
解法2:∵设{an}为等差数列,
∴sm,s2m-sm,s3m-s2m成等差数列,
即30,70,s3m-100成等差数列,
∴30+s3m-100=70×2,
解得s3m=210.
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,定义向量
,定义向量 ,
,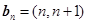 ,
,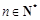 . 下列命题中真命题是
. 下列命题中真命题是 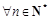 总有
总有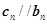 成立,则数列
成立,则数列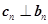 成立,则数列
成立,则数列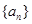 满足
满足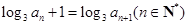 且
且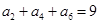 ,则
,则 的值是
的值是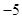
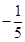
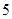
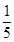
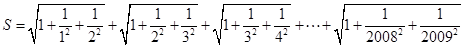 ,则不大于S的最大整数[S]等于()
,则不大于S的最大整数[S]等于()  为等差数列,前
为等差数列,前 项和为
项和为 ,已知
,已知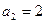 ,
,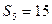 ,
,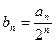 ,求数列
,求数列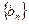 的前
的前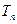 .
.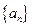 满足:
满足: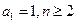 时,
时,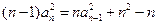 。
。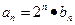 ,数列
,数列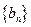 的前n项和为
的前n项和为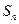 ,是否存在正整数m,使得对任意的
,是否存在正整数m,使得对任意的
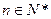 ,
,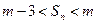 恒成立?若存在,求出所有的正整数m;若不存在,说明理由。
恒成立?若存在,求出所有的正整数m;若不存在,说明理由。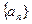 是等差数列,
是等差数列,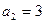 ,
,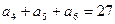 ,
,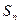 为数列
为数列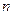 项和
项和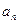 和
和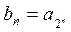 ,求数列
,求数列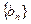 的前
的前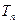
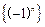 的前
的前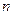 项和为
项和为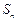 ,则对任意正整数
,则对任意正整数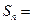
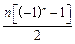
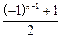
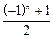
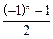
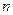 行有
行有
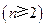 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如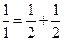 ,
, ,
,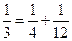 ,…,则第7行第4个数(从左往右数)为( )
,…,则第7行第4个数(从左往右数)为( )