Question

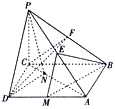
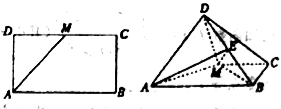
【题目】如图，已知长方形中，为的中点，将 沿折起，使得平面平面．

（1）求证：；

（2）若点是线段上的一动点，问点在何位置时，三棱锥的体积与四棱锥的体积之比为1：3？

Answer 1

【答案】（1）详见解析（2）为的中点

【解析】

试题分析：（1）证明线线垂直，一般利用线面垂直判定与性质定理，经多次转化得证.其中线线垂直的寻找与论证，一般从两个方面出发，一是平几知识，如本题中利用长方形长与宽的关系得，另一方面，利用立几中线面垂直关系进行转化，如由面面垂直转化为线面垂直，再转化为线线垂直（2）研究体积关系，一般利用等体积法进行转换：，所以，因此为的中点

试题解析：（1）证明：∵长方形中，为的中点，∴，∴，

∵平面平面，平面平面平面，

∴平面，∵平面，∴

（2）为的中点，

当为的中点时，因为，

所以