题目内容
【题目】设数列{an}满足:a1=1,且当n∈N*时,an3+an2(1﹣an+1)+1=an+1.
(1)求a2,a3的值;
(2)比较an与an+1的大小,并证明你的结论.
(3)若bn=(1![]() )
)![]() ,其中n∈N*,证明:0<b1+b2+……+bn<2.
,其中n∈N*,证明:0<b1+b2+……+bn<2.
【答案】(1)a2![]() ,a3
,a3![]()
![]() ;(2)an+1>an;见解析(3)见解析
;(2)an+1>an;见解析(3)见解析
【解析】
(1)由已知数列递推式得出an+1![]() ,依次代入计算可得a2,a3的值;
,依次代入计算可得a2,a3的值;
(2)利用作差![]() ,通分后配方可证明an+1>an;
,通分后配方可证明an+1>an;
(3)由于bn=(1![]() )
)![]() ,且an+1>an,得
,且an+1>an,得![]() 0,由an+1>an>…>a1=1>0得bn>0,从而可得b1+b2+……+bn>0;再由bn=(1
0,由an+1>an>…>a1=1>0得bn>0,从而可得b1+b2+……+bn>0;再由bn=(1![]() )
)![]()
![]() ,得到bn
,得到bn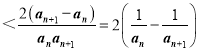 .利用裂项相消法得
.利用裂项相消法得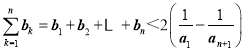 ,从而可证得结论.
,从而可证得结论.
(1)解:依题意,由an3+an2(1﹣an+1)+1=an+1,可解得an+1![]() ,
,
则a2![]() ,
,
a3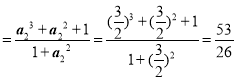 ;
;
(2)解:an+1>an.
证明如下:
由(1)得an+1![]() ,
,
∴an+1﹣an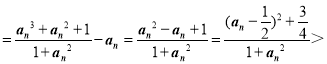 0,
0,
∴an+1>an;
(3)证明:由于bn=(1![]() )
)![]() ,
,
由(1)an+1>an,则![]() 1,
1,![]() 0,
0,
而an+1>an>…>a1=1>0,则bn>0,
∴![]() 0.
0.
又于bn=(1![]() )
)![]()
![]() ,
,
∴bn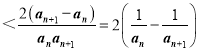 .
.
∴![]() 2[(
2[(![]() )+(
)+(![]() )+…+(
)+…+(![]() )],
)],
∴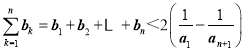 ,
,
而an+1>an,且a1=1,故an+1>0.
∴![]() ,从而0<b1+b2+……+bn<2.
,从而0<b1+b2+……+bn<2.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目